Cum să adăugați forțe paralele care acționează asupra unui corp solid
Când în paginile anterioare am rezolvat problemele mecanicii, în care corpul a fost înlocuit mental cu un punct, întrebarea de adăugare a forțelor a fost rezolvată pur și simplu. Regula de paralelogramă a dat un răspuns la această întrebare, iar dacă forțele erau paralele, am adăugat amploarea lor ca numere. Acum lucrurile sunt mai complicate. La urma urmei, efectul forței asupra unui obiect se caracterizează nu numai prin magnitudinea și direcția sa, ci și prin punctul de aplicare a acestuia, sau - am explicat mai sus că aceasta este aceeași - linia de acțiune a forței.
A combina forțele înseamnă a le înlocui cu una. Acest lucru nu este întotdeauna posibil.
Înlocuirea forțelor paralele ale unui singur rezultat este o sarcină care este întotdeauna fezabilă (cu excepția unui caz special, care va fi discutat la sfârșitul acestei secțiuni). Luați în considerare adăugarea de forțe paralele. Bineînțeles, suma forțelor în 3 kg și 5 kg este de 8 kg dacă forțele privesc într-o direcție. Sarcina este de a găsi punctul de aplicare (linia de acțiune) a rezultatului.
În Fig. 54 arată două forțe care acționează asupra corpului. Forța totală F înlocuiește forțele F1 și F2. Dar aceasta înseamnă nu numai că F = F1 + F2. acțiunea forței F va fi echivalentă cu acțiunea lui F1 și F2 în cazul în care momentul forței F este egal cu suma momentelor F1 și F2.
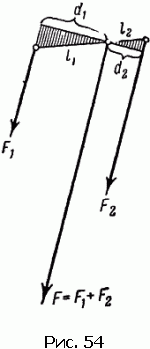
Căutăm o linie de acțiune a forței totale F. Desigur, este paralelă cu forțele F1 și F2. Dar la ce distanțe trece această linie din forțele F1 și F2?
Ca punct de aplicare al forței F în figură, este prezentat un punct care se află pe segmentul care leagă punctele de aplicare a forțelor F1 și F2. În ceea ce privește punctul ales, instantaneul F este, desigur, zero. Dar atunci suma momentelor F1 și F2 față de acest punct trebuie să fie și zero, adică momente ale forțelor F1 și F2. opuse în semn, vor fi egale în magnitudine.
Din similitudinea triunghiurilor umbrite rezultă că d2 / d1 = l2 / l1. și anume Punctul de aplicare a forței totale pe segmentul de conectare împarte distanța dintre forțele pliate în părțile 11 și 12. invers proporțional cu forțele.
Rezolvăm sistemul a două ecuații cu două necunoscute:
Conform acestor formule, putem găsi punctul de aplicare a forței rezultante nu numai atunci când forțele se uită într-o direcție, ci și în cazul forțelor îndreptate în direcții opuse (se spune că sunt antiparalerale). Dacă forțele sunt direcționate în direcții diferite, atunci ele au semne opuse, iar rezultatul este egal cu diferența dintre forțele F1. F2. dar nu suma lor. Presupunând că cea mai mică dintre cele două forțe este negativă, F2. vedem prin formulele noastre că l1 devine negativ. Aceasta înseamnă că punctul de aplicare al forței F1 nu se află spre stânga (ca mai înainte), ci spre dreapta punctului de aplicare al rezultatului (Figura 55), în timp ce încă
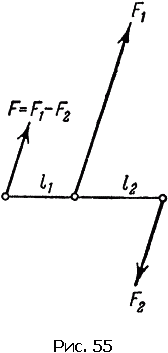
Un rezultat interesant este obținut cu forțe egale antiparallel. Apoi F1 + F2 = 0. Formulele arată că l1 și l2 devin infinit de mari. Care este semnificația fizică a acestei afirmații? Deoarece nu are rost să ne referim rezultatul la infinit, înseamnă că forțele egale antiparallel nu pot fi înlocuite de una. Această combinație de forțe este numită o pereche de forțe.
Acțiunea unei perechi de forțe nu poate fi redusă la acțiunea unei forțe. Orice două forțe paralele sau antiparalerale pot fi echilibrate de una și o pereche de forțe - este imposibil.
Desigur, ar fi incorect să spunem că forțele care alcătuiesc perechea se distrug unul pe altul. O pereche de forțe are un efect foarte semnificativ - rotește corpul; trăsătura acțiunii unei perechi de forțe este aceea că nu dă mișcare înainte.
În unele cazuri, nu se poate pune întrebarea despre adăugarea forțelor paralele, ci despre descompunerea unei forțe date în două forțe paralele.
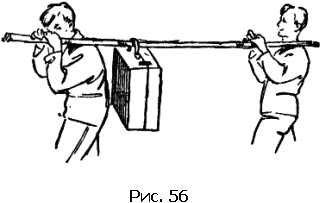
În Fig. 56 arată doi oameni care împreună poartă un valiziu greu pe un baston. Greutatea valizei este descompusă pe ambele. Dacă încărcătura se apasă pe mijlocul bățului, atunci ambii experimentează aceeași gravitate. Dacă distanța de la punctul de aplicare a încărcăturii la mâinile care o poartă, d1 și d2. atunci forța F se descompune în forțele F1 și F2 prin regulă
Oricine este mai puternic, trebuie să ia bastonul mai aproape de încărcătură.
Distribuiți această pagină