
Acasă | Despre noi | feedback-ul
Luați în considerare un conductor solitar, adică un conductor care este îndepărtat de alte conductori, corpuri și încărcături. Potențialul său, conform (84.5), este direct proporțional cu sarcina conductorului. Din experiență rezultă că diferiți dirijori, fiind încărcați în mod egal, își asumă diferite potențiale. Prin urmare, pentru un produs solitar putem scrie Q = Cj. Suma
C = Q / j (93.1) se numește capacitatea electrică (sau pur și simplu capacitatea) unui conductor solitar. Capacitatea unui conductor solitar este determinată de încărcătura, mesajul căruia îi schimbă potențialul printr-o singură dată. Capacitatea conductorului depinde de dimensiunea și forma sa, dar nu depinde de material, starea agregată, forma și dimensiunile cavităților din interiorul conductorului. Acest lucru se datorează faptului că încărcăturile excesive sunt distribuite pe suprafața exterioară a conductorului. Capacitatea nu depinde nici de încărcarea conductorului, nici de potențialul acestuia. Aceasta nu contravine formulei (93.1), deoarece arată doar că capacitatea unui conductor solitar este direct proporțională cu sarcina sa și este invers proporțională cu potențialul. Unitatea de capacitate electrică este Farad (Ф): 1 Φ este capacitatea unui astfel de conductor solitar, a cărui potențial se modifică cu 1 V când sarcina îi este dată în 1 CI. În conformitate cu (84.5), potențialul unui balon solitar de rază R într-un mediu omogen cu permitivitate dielectrică e este egal cu
Folosind formula (93.1), obținem capacitatea mingii
Rezultă că capacitatea de 1 F raidurilor făcute bilă intim situat în vid și având o rază R = C / (4pe0) »9 • Iunie 10 km, care este de aproximativ 1400 de ori mai mare decât raza Pământului (electron-troemkost Pământ C“ 0,7 mF). În consecință, TION, Faraday - o valoare foarte mare, astfel încât, în practică, utilizate pe lungime de unități Nye - mf (MF), micro-farazi (uF), nF (nF), picofarads (pF).. De asemenea, rezultă din (93.2) că unitatea de constante electrice electrice e0 per metru (F / m) (a se vedea (78.3)).
După cum se poate observa din § 93, pentru ca un conductor să aibă o capacitate mare, acesta trebuie să aibă dimensiuni foarte mari. În practică, cu toate acestea, dispozitivele care au capacitatea de a acumula sarcini semnificative de mici dimensiuni și mici față de corpurile din jur sunt necesare, cu alte cuvinte, să aibă o capacitate mare. Aceste dispozitive sunt numite condensatoare.
În cazul în care un conductor încărcat cu aproape de alt organism, atunci acestea apar induse (pe conductorul) sau con asociat (în dielectric) taxe, cel mai apropiat de taxa Q sugestive tarifele Bu FLS de semn opus. Aceste taxe sunt atenuează în mod natural de câmp cos ef dat de Q, r. E. inferior în potențialul conductorului, care rezultate (vezi. (93,1)) creșterea capacității sale electrice.
Condensatorul este alcătuit din două conductoare (plăci) separate printr-un dielectric. Capacitatea condensatorului nu trebuie să fie afectată de corpurile înconjurătoare, astfel încât conductorii sunt formați astfel încât câmpul creat de încărcăturile acumulate să fie concentrat în decalajul îngust între plăcile condensatoarelor. Această condiție este îndeplinită (vezi § 82): 1) două plăci plate; 2) doi cilindri coaxiali; 3) două sfere concentrice. Prin urmare, în funcție de forma plăcilor, condensatoarele sunt împărțite în formă plană, cilindrică și sferică.
Deoarece câmpul este concentrat în interiorul condensatorului, liniile de tensiune încep pe o placă și se termină pe cealaltă, astfel încât încărcăturile libere care apar pe plăci diferite sunt egale în modul cu încărcături opuse. Sub capacitatea condensatorului, se ia în considerare o cantitate fizică egală cu raportul dintre sarcina Q acumulată în condensator și diferența de potențial (j1 -j2) între plăcile sale: C = Q / (j1 -j2). (94.1)
Calculăm capacitatea unui condensator plat format din două plăci metalice paralele, cu o suprafață de 5 fiecare, situate la o distanță d una de cealaltă și având încărcări + Q și -Q. Dacă distanța dintre plăci este mică în comparație cu dimensiunile lor liniare, atunci efectele de margine pot fi neglijate, iar câmpul dintre plăci considerat omogen. Se poate calcula folosind formulele (86.1) și (94.1). În prezența unui dielectric între plăci, diferența de potențial dintre acestea, în conformitate cu (86.1),
unde e este permitivitatea. Apoi din formula (94.1), înlocuind Q = sS, luând în considerare (94.2) se obține expresia pentru capacitatea unui condensator plat:
Pentru a determina capacitatea unui condensator cilindric care este alcătuit din doi cilindri tubulari coaxiali cu r1 raze și r2 (r2> r1), inserată într-un altul, din nou prehnite- Neglija efecte de margine, considera câmp radial simetric și centrată între electrozii cilindrice. Diferența de potențial între electrozi calculat prin formula (86.3) pentru câmpul este încărcat TION uniform a unui cilindru infinit cu liniar bine-Stu t = Q / l (l este lungimea plăcilor). Având în vedere prezența unui dielectric între plăci
Înlocuind (94.4) în (94.1), obținem o expresie pentru capacitatea unui condensator cilindric:
Pentru a determina capacitatea sferică con-condensator, care este format din doi electrozi concentrice separate de un strat sferic electrics di-, utilizați formula (86.2) pentru potențialul timp de suprafață între două puncte situată conductoare la distanțe de r1 și r2 (r2> r1) din centrul suprafața sferică încărcată. Având în vedere prezența unui dielectric între plăci
Înlocuind (94.6) în (94.1), obținem
Dacă d = r2-r1<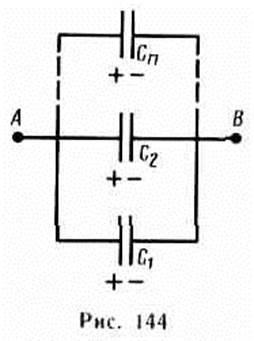
Condensatoarele sunt caracterizate printr-o tensiune de rupere - diferența de potențial între plăcile de condensatoare, la care se produce defectarea - o descărcare electrică prin stratul dielectric din condensator. Tensiunea de descompunere depinde de forma plăcilor, de proprietățile di-electrice și de grosimea acestora.
Pentru a mări capacitatea și a modifica valorile posibile, condensatoarele sunt conectate la baterii, utilizând conexiunea lor paralelă și serială.
1. Racordarea paralelă a condensatoarelor (Figura 144). În condensatoarele conectate în paralel, diferența de potențial pe plăcile condensatoarelor este aceeași și este egală cu jA -jB. Dacă capacitățile condensatoarelor individuale C1, C2. Cn, atunci, în conformitate cu (94.1), taxele lor sunt egale cu
Capacitatea maximă a bateriei
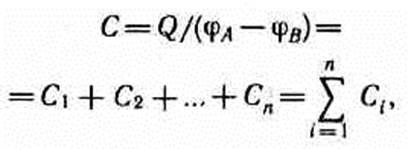
adică atunci când condensatorii sunt conectați în paralel, este egal cu suma capacităților condensatoarelor individuale.
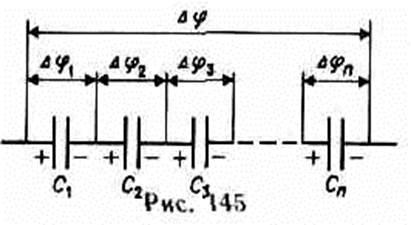
2. Conectarea consecventă a condensatoarelor (Figura 145). La condensatoarele seriale conectate, sarcinile tuturor plăcilor sunt egale în modul și diferența de potențial la bornele bateriei
unde pentru oricare dintre condensatoarele considerate
Pe de altă parte,
adică, atunci când condensatoarele sunt conectate în serie, se adaugă cantitățile opuse capacităților. Astfel, atunci când condensatoarele sunt conectate în serie, capacitatea rezultantă C este întotdeauna mai mică decât cea mai mică capacitate utilizată în baterie.