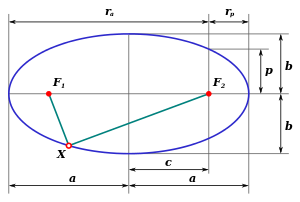
Parametrii de bază ai elipsei
Axa principală a elipsei este diametrul său cel mai mare - segmentul care trece prin centru și două focare. Axa semimajor este la jumătatea distanței și se deplasează de la centrul elipsei prin focalizare la marginea sa.
La un unghi de 90 ° față de semiaxis se află axa semimajor - distanța minimă de la centrul elipsei până la marginea ei. În cazul special al unui cerc de elipse, semiaxurile mari și mici sunt egale și sunt raze. Astfel, putem considera semiaxurile mari și minore ca fiind niște raze ale elipsei.
Lungimea semiaxelor majore este legată de lungimea axei minore prin excentricitatea, parametrul focal și distanța focală (jumătate distanța dintre focare) după cum urmează:
Axa semimajor este media aritmetică dintre distanțele de la orice punct al elipsei până la focare.
Având în vedere ecuația în coordonate polare. cu un punct la origine (pol) și o rază pornind de la acest punct (axa polare):
Obținem valorile medii ale u și axei semimajor
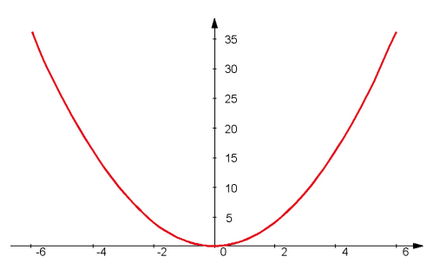
Parcela construirii unei parabole cu cea mai simplă funcție y = x 2
O parabolă poate fi obținută ca limită a unei secvențe de elipse, unde o focalizare rămâne constantă, iar cealaltă este retrasă până la infinit, menținând-o constantă. Astfel, au tendința de a infinit, și mai repede decât.
Axa semimajor a hiperboliei este jumătate din distanța minimă dintre cele două ramuri ale hiperboliei, pe părțile pozitive și negative ale axei (stânga și dreapta față de origine). Pentru o sucursală situată pe partea pozitivă, semiaxisul va fi:
Dacă o exprimăm printr-o secțiune conică și excentricitate, atunci expresia ia forma:
.
O linie dreaptă care conține axa majoră a unei hiperbola este numită axa transversală a hiperbolei. [1]
astronomie
Perioada orbitală
În mecanica cerească, perioada orbitală de revoluție a corpurilor mici într-o orbită eliptică sau circulară în jurul unui corp central mai mare se calculează prin formula:
Este dimensiunea axei semimajor a orbitei - acesta este parametrul gravitațional standard
Trebuie notat faptul că în această formulă pentru toate elipsele perioada de rotație este determinată de valoarea axei semimajor, indiferent de excentricitate.
În astronomie, axa semimajor, împreună cu perioada orbitală. este unul dintre cele mai importante elemente orbitale ale orbitei corpului cosmic.
Pentru obiectele sistemului solar, axa semimajor este legată de perioada orbitală conform celei de-a treia legi a lui Kepler.
- perioada orbitală în ani; - Axa semimajor în unitățile astronomice.
Această expresie este un caz special al soluției generale a problemei cu două corpuri a lui Isaac Newton.
- constanta gravitationala - masa corpului central - masa satelitului din jurul acestuia. De regulă, masa satelitului este atât de mică în comparație cu masa corpului central încât poate fi neglijată. Prin urmare, prin simplificări adecvate în această formulă, obținem această formulă într-o formă simplificată, care este dată mai sus.
Orbita mișcării prin satelit în jurul centrului de masă comun al corpului central (barycenter) este o elipsă. Axa semimajor este folosită în astronomie întotdeauna cu referire la distanța medie dintre planetă și stea, ca urmare a orbitelor planetelor sistemului solar fiind reduse la sistemul heliocentric. și nu unui sistem de mișcare în jurul centrului de masă. Această diferență este ilustrată cel mai bine de exemplul sistemului Pământ-Lună. Raportul de masă în acest caz este 81.30059. Axa semimajor a orbitei geocentrice a Lunii este de 384.400 km. în timp ce distanța față de Lună față de centrul de masă al sistemului Pământ-Lună este de 379.700 km - datorită influenței masei Lunii, centrul de masă nu se află în centrul Pământului, ci la o distanță de 4700 km de ea. Ca rezultat, viteza orbitală medie a Lunii față de centrul de masă este de 1.010 km / s, iar viteza medie a Pământului este de 0.012 km / s. Suma acestor viteze dă viteza orbitală a lunii de 1.022 km / s; aceeași valoare poate fi obținută prin luarea în considerare a mișcării lunii față de centrul Pământului, și nu a centrului de masă.