
Acasă | Despre noi | feedback-ul
Prin definiție, densitatea unei variabile aleatorii distribuite normal este
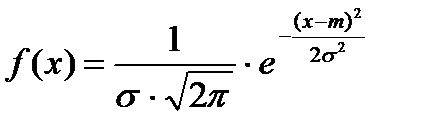
Valorile posibile ale unei astfel de valori a lui X pot lua orice valoare reală -∞<Х<∞, а распределение зависит от двух параметров. -∞ Astfel, graficul funcției f (x) va fi după cum urmează: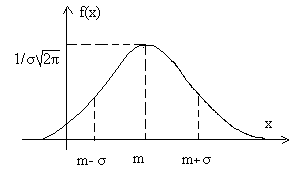
Dacă m = 0 și # 963; = 1. atunci legea distribuției normale se numește standard. În acest caz
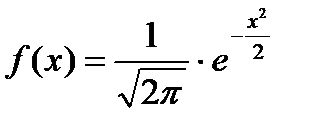
Dacă variabila aleatoare X este distribuită conform legii normale cu parametrii m și # 963; atunci acest fapt este scris astfel.
Calculați așteptările matematice ale unei variabile aleatorii
Astfel, parametrul m este așteptarea matematică a variabilei aleatoare X.
Acum calculam variația
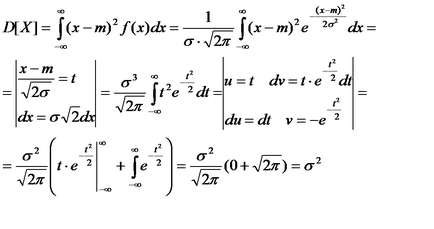
unde am folosit ceea ce se întâmplă în conformitate cu regula lui L'Hospital
Astfel, parametrul # 963; este abaterea standard, deoarece # 963; 2 este variația.
Modul și media distribuției normale coincid cu așteptările matematice, deoarece Maximul f (x) este atins la x = m și
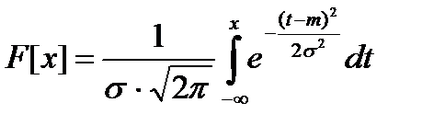
funcția de distribuție a legii care are graficul prezentat în figură.
Să calculăm P (a<Х unde am folosit formula Newton-Leibniz pentru integrale definite, și este orice antiderivativă pentru integrad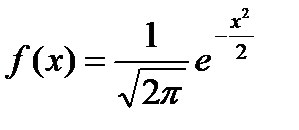
Orice derivat antiderivativ poate fi calculat din formula
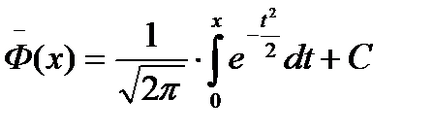
unde C este o constantă arbitrară. Acest lucru poate fi ușor verificat prin diferențiere.
Pentru C = 0 obținem funcția Laplace
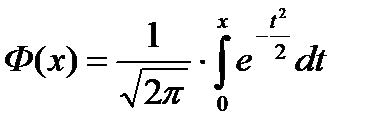
și pentru C = ∞, funcția de distribuție a normei normale standard
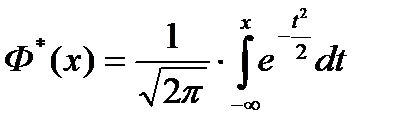
În funcție de tabelele pe care le avem la dispoziție, vom folosi una sau o altă formulă. Observăm că este mai convenabil să folosim tabelele funcției Laplace, deoarece este ciudat și suntem ușor - găsim valorile sale pentru un argument negativ (de obicei tabelele sunt date doar pentru valorile pozitive ale argumentului). Folosirea tabelelor pentru funcția Φ * (χ) în acest caz este oarecum mai inconvenientă dacă este dată numai pentru valorile pozitive ale argumentului.
EXEMPLUL 1. Să găsim probabilitatea ca X să ia o valoare din intervalul 0, 3 [.
Prin tabelul funcției Laplace obținem
Prin tabelul funcției de distribuție a legii normale standard obținem, folosind legătura sa cu funcția Laplace:
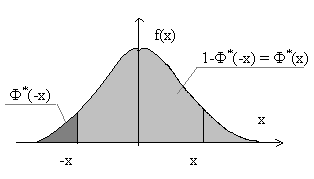
care este ușor de explicat prin figura următoare.
Să găsim probabilitatea ca o variabilă aleatorie normală să cadă în intervalul m-1, m + l [simetric față de așteptările matematice:
Pentru diferite valori ale lui l obținem
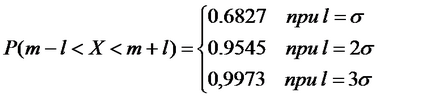
După cum vedem, deși valorile teoretic posibile ale lui X pot fi arbitrare, dar practic toate valorile intră în intervalul m-3 # 963 ;, m + 3 # 963; Acest fapt este de obicei numit regula "trei sigma". Cu o distribuție normală de 10.000 de măsurători, numai 27 au dreptul "legitim" de a părăsi acest interval (un eveniment puțin probabil și de obicei neglijat). Prin urmare, putem presupune că toate valorile posibile ale unei variabile aleatorii normale sunt în acest interval.