373. Patru monede. Ia 4 monede identice și puneți-le pe masă fără ajutorul altor monede sau alte ajutoare, astfel încât a cincea moneda poate fi potrivi cu exactitate la cele patru date fără a se deplasează acesta din urmă (cercul hașurată reprezintă a cincea monedă).
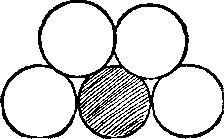
Bazându-se doar pe ochiul tău, cel mai probabil vei eșua. În același timp, condiția poate fi îndeplinită cu exactitate absolută. Dar cum?
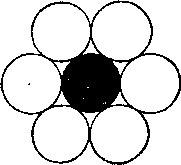
374. Șase monede. Se pune 6 din aceeași monedă pe masă, apoi așezați-le așa cum este arătat prin cercuri deschise, astfel încât moneda a șaptea coborât (cerc negru) în centru, v-ar fi adus-o astfel în contact cu toate cele șase monede. Sarcina trebuie să fie executată exact, nu "prin ochi". Ridicați orice monedă din tabel (altfel nu ar fi primit nici un puzzle-uri) sau pentru a efectua orice măsurători nu sunt permise. Numai șase monede sunt la dispoziția dumneavoastră.
Probleme combinatoriale și topologice
375. Pătrat magic magic. Cifra prezentată aici prezintă pătratul magic magic, compus din numere de la 1 la 16 inclusiv. Suma numerelor în orice rând, orice coloană și oricare dintre cele două diagonale mari este egală cu 34. Acum presupunem că nu au voie să folosească numerele 2 și 15, dar în schimb se poate duplica oricare două numere deja utilizate anterior.

Cum ar trebui să fie aranjate numerele astfel încât, în noul pătrat, sumele lor în toate rândurile, coloanele și diagonalele să fie în continuare egale cu 34? Succesul depinde de numerele pe care le înlocuiți 2 și 15.
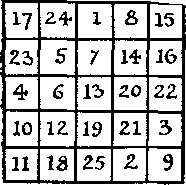
376. Neînțelegere cu un pătrat magic. În fața ta este un patrat magic al ordinii a cincea. Am constatat că marea majoritate a oamenilor nu sunt familiarizați cu teoria patrate magice profunde, convins, ca și în cazul în care într-o pătrate cincea ordine în centrul numărul 13. Un cititor trebuie să stea în mod necesar de mai mulți ani amuzat de această piață, a fost uimit când a învățat de la mine că în centrul unui astfel de pătrat poate sta orice număr de la 1 la 25.
Dovediți că acest lucru este într-adevăr așa. Încercați, de exemplu, să creați un pătrat magic magic, în centrul căruia ar fi 1.

377. Diferența pătrate. Poți plasa 9 numere într-un pătrat, astfel încât, în fiecare rând, fiecare coloană și în fiecare din diferența diagonalele mare între suma celor două numere, iar cifrele a treia se potrivesc unele cu altele? În această figură este prezentat un pătrat, în care toate liniile și coloanele sunt satisfac condiția necesară - diferența în ele este 3 (de exemplu, 4 + 2 - 3, 1 + 9 - 7 6 + 5 - .. 8, etc.), dar diagonal „pompat în sus“, din cauza diferenței de 8 - (4 + 1) și 6 - (1 + 2) obținut manieră proscriși nu una dintre cifrele trebuie deduse suma celorlalte două, iar suma a doi - unu.
Câte decizii există?
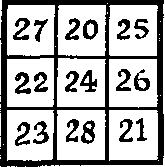
378. Este atât de simplu? Aici este un simplu pătrat magie, suma care numere de la orice linie din orice coloană pe principalele diagonalele sunt egale cu 72. puzzle este de a transforma într-un pătrat magic multiplicativ, al căror număr de produse de la orice bar, în orice coloană sau pe oricare dintre diagonalele mari, ar coincide unele cu altele. Nu este permis să schimbați numerele în funcție de locații, să adăugați ceva la ele sau să utilizați semne aritmetice la toate! Puteți muta numai numerele din interiorul aceleiași celule. Deci, în loc de 27 este permis să ia 72.
Dacă reușiți să găsiți "cheia" soluției, sarcina va fi neobișnuit de simplă. Altfel, rezolva puzzle-ul este aproape imposibil.
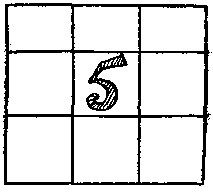
Se umple pătrate (a se vedea. Figura) Numerele (în fiecare caz diferit, astfel încât nu există două celule nu conțin aceleași cifre), astfel încât suma numerelor care este posibil într-un număr mai mare de coloane și rânduri pe diagonalele, egală cu 15. În timpul indiciul „secreție „focus a fost numit ca marele premiu, dar pentru a obține soluția corectă nu este posibilă pe nimeni.
Poate cititorul va decide care este problema aici?

380. Pătratul magic de patru figuri. Întrucât pătratul dat este alcătuit din același număr 1234, este normal ca sumele numerelor în toate rândurile, coloanele și diagonalele să fie egale. Esența puzzle-ului este de a compune și plasa 9 numere diferite de patru cifre (compuse din aceleași patru cifre) astfel încât să formeze și pătratul magic magic. Amintiți-vă că, împreună, numerele trebuie să conțină nouă copii ale fiecăreia dintre cifrele 1, 2, 3, 4 și că acestea ar trebui să fie numere reale de patru cifre fără fracțiuni; nu sunt permise trucuri aici.
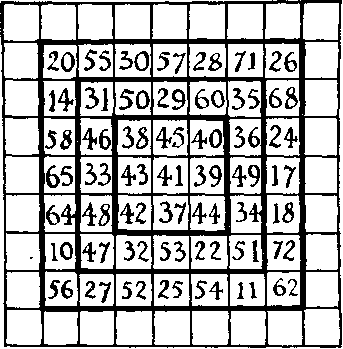
Piețe progresive. Aici este un pătrat de magie, care este constantă, adică suma numerelor din fiecare rând, fiecare coloană și fiecare dintre cele două diagonale este egal cu 287. Dacă eliminăm numărul situat pe margini, acesta va fi un alt constantă pătrat magic este egal cu 205. În cazul în care vom elimina din nou numerele extreme, veți obține pătrat cu constanta 123. acum Umple celule goale cu numere 1-83 inclusiv, astfel încât să se obțină un pătrat cu o constantă magică 369 la oricare dintre cele 20 de linii sale.
382. Pătrat magic magic. Deși nu există nimic de adăugat în legătură cu construcția simplă a pătratelor magice, și există o literatură foarte extinsă asupra subiectului însuși, deși este o literatură împrăștiată, variații mici, cu unele condiții noi, întotdeauna provoacă interes. Iată un exemplu simplu.

Se poate construi un pătrat de magie, a cărui sumă a numerelor în orice rând, orice coloană, și pe fiecare dintre cele două diagonale mari, ar fi fost la fel, de numere de la 1 la 25, dacă sunt introduse în celulele umbrite doar numere impare inclusiv, și restul sunt chiar? Există multe soluții la această problemă. Puteți găsi cel puțin una dintre ele?
383. Steaua cu cinci puncte. Puzzle-ul cu stelele au un fel de forță atrăgătoare. Voi da un exemplu al unui astfel de puzzle cu o stea simplă cu cinci puncte.
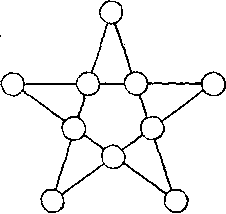
În fiecare cerc stea cu cinci colțuri prezentate aici trebuie să numere diferite, astfel încât suma oricăror patru numere pe aceeași linie dreaptă, egală cu 24. Soluții cu zece numere consecutive nu există, dar puteți utiliza oricare dintre numere întregi, pe care le doriți.
384. Stea cu șase puncte. În problema anterioară, am considerat cazul unei stele cu cinci puncte. Se pare că situația cu steaua cu șase puncte este chiar mai interesantă. În acest caz (a se vedea. Figura), putem folosi întotdeauna cele 12 numere consecutive 1 - 12 și suma celor patru numere pe fiecare linie va fi întotdeauna egal cu 26. Suma numerelor din cele șase vârfuri pot fi orice număr 24-54 inclusiv cu excepția 28 și 50. În acest exemplu, această sumă este egală cu 24. În cazul în care, în loc de fiecare dintre numerele pe care le Substituind diferența dintre el și 13, veți obține o soluție diferită, ca urmare a acestui fapt, suma nodurilor egal cu 54 (78 minus 24). Două sume suplimentare din total se datorează întotdeauna 78.