Amintiți-vă geometria. Ecuația cercului are forma:
a, b sunt coordonatele centrului cercului
R este raza cercului
Ecuația unui cerc de rază R cu centrul la origine:
Acest lucru ne va ajuta să cunoaștem variabilele într-o altă reprezentare a cercului: în ecuația parametrică:
în centrul coordonatelor:
Vedem date familiare și altele: alpha. Cred că este clar că acesta este un colț. Modificați unghiul alfa și obțineți mișcarea de-a lungul cercului.
Toate acestea sunt transferate la Unitate.
Să presupunem că, la un moment dat în timp, este necesar ca obiectul a început să se miște într-un cerc, și, prin urmare, trebuie să se schimbe unghiul și, treptat, se transferă valoarea în coordonatele. Unghiul poate fi modificat, de exemplu, în Actualizare. care va fi numit fiecare cadru. Apoi vom obține o formulă simplă:
Când trebuie să opriți mișcarea într-un cerc, setați Ciclul la fals și la zero unghiul unghiului = 0;
Pentru a vă deplasa într-un centru, nu uitați să adăugați această condiție la coordonate. De exemplu, un centru cu coordonatele 1, 1,5; Formula va fi astfel:
În sens orar sau în sens contrar acelor de ceasornic?
Totul este simplu aici. Una dintre coordonate trebuie înmulțită suplimentar cu -1. Dacă înmulțiți X, atunci mișcarea va merge ca și cum ați fi la 180 °
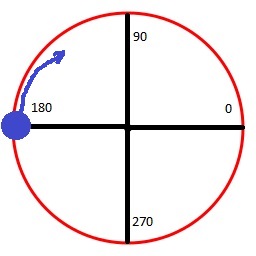
Dacă înmulți Y, atunci de la 0 °:
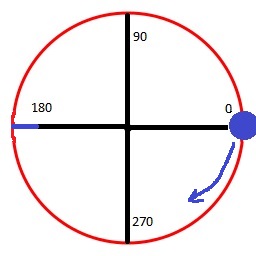
Dacă nu confundăm nimic))
Aici este o mișcare înainte banală și foarte prime a corpului, și atunci când modificați parametrul isCircle la muștele adevărat invers acelor de ceasornic exact la locul unde există (pentru aceasta în formula este o altă opțiune nouă Vector2 (rază, 0) pentru a compensa direcția de mișcare).
Ei bine, despre mișcarea pe sinusoid. Aici puțin diferit. Pe o axă, ne mișcăm, iar pe de altă parte, ca să spunem așa, "încurcă".
Voi incerca sa scriu doar doua formule, incercati sa le rezolvati singuri)))
1) Mutarea înainte, "încurcarea" în jos: