Bună ziua, dragi studenți ai Universității Argemon!
M-am gândit cum să folosesc bagheta magică pentru a muta obiecte. Nu fiecare obiect și nu fiecare magician poate trece de la un loc la altul. Este clar că cu cât obiectivul este mai ușor, cu atât este mai ușor să îl ridicați în aer. Puteți aminti exemplul clasic din lumea lui Harry Potter, studenții studiind vraja "Wingardium of Levios", încercând să ridice o pene. Acolo, și un val de mână este sigur, și este nevoie de pronunția corectă a vrajii, desigur.
Cu toate acestea, cum funcționează mecanismul baghetelor? Coli, după cum știm, este o continuare a mâinile unui magician, și care curge prin ea, și rupe în direcția energiei magice obiectului dorit, care ar trebui, de exemplu, în cazul de față pentru a ridica subiectul. Cum acționează această energie asupra obiectului? Plicurile sunt întregi și o ridică? Sau într-un fel diferit?
Există un astfel de concept pentru orice obiect ca centru al masei. Acesta este punctul care caracterizează mișcarea corpului în ansamblu. Adică atunci când corpul se mișcă, se poate lua în considerare numai mișcarea centrului său de masă, pentru care toate legile fizicii mișcării sunt îndeplinite. Și imediat există un gând. Apoi acțiunea baghetei ar trebui să fie îndreptată numai spre acest centru de masă, bine, sau pe o zonă mică, acest punct înconjurător?
Deci, de fapt, este nevoie de mult mai puțin efort pentru a muta corpul.
Acestea sunt doar gândurile mele și aș vrea să aud și a ta. Poate că m-am înșelat în ceva sau ceva ce nu o consider.
Și în această lecție vom căuta doar centrul de masă pentru trapezoizii curbilinari. Acordați atenție: nu încă pentru o curbă arbitrară a figurii, și anume pentru trapezoidul curbilinar.
În general, vrăji pentru a găsi acest punct nu sunt foarte complicate
S este zona trapezului curbilinar, pe care am învățat-o deja să o găsim.
Pentru a fi mai clară, să luăm în considerare exemple de trapezuri curvilineare din prelegerea precedentă.
Exemplul 1. Găsiți centrul de masă al unei figuri delimitată de un val de cosinus
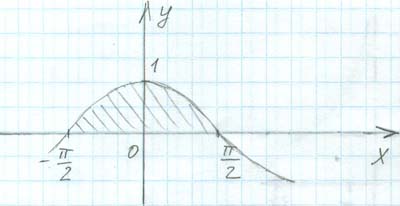
Aria acestei cifre, pe care am calculat-o deja, este egală cu 2. Acum, folosind formulele conjurative menționate mai sus, se calculează coordonatele centrului de masă.
Se vede că centrul de masă pentru această figură simetrică se află pe axa OU la o altitudine de aproximativ 0,4.
Exemplul 2. Și acum, uitați-vă la figura curbilinie formată din două trapezoide curbilinii.
În acest caz, este necesar să se calculeze centrele de masă pentru fiecare trapez.
Avem două centre de masă. Acum trebuie să găsim centrul de masă al celor două puncte obținute, care sunt mase de trapeze noastre curbilinii concentrate (în acest caz, zona pentru că figura plat). Punctul C1 este concentrată întreaga suprafață a trapezului curbat stânga, la punctul C2 - zona curbată trapezoid dreapta (care este un triunghi isoscel dreptunghiular).
In general, pentru o formulă de greutate corporală este: m = ρ * V, adică pentru figura dimensională de grosime constantă trebuie încă calculat volumul (zona înmulțită cu grosimea) și apoi folosind densitatea materialului, pentru a calcula masa.
Dar încă avem în vedere corpuri plate.
Conectăm două puncte. Acestea sunt puncte materiale - doar cele în care se concentrează întreaga masă a corpului dat. Centrul de masă căutat este căutat de regula pârghiei arhimede. Produsul masei unui punct material, distanța de la acesta la centrul de masă, este același pentru ambele puncte; m1 * d1 = m2 * d2. unde m1 și m2 sunt masele punctelor materiale și d1. d2 - umerii corespunzători.
Mai intai trebuie sa gasim lungimea segmentului care ne conecteaza punctele. Deoarece punctele au coordonate exacte, lungimea segmentului este căutată pur și simplu de formula
Și acum luăm d1 pentru t, apoi d2 = 0.58-t
Sa dovedit că centrul de masă al figurii noastre este la o distanță de 0.348 de punctul C1. și aceasta va fi în zona trapezului drept.
Să calculăm cât de mult din acest segment este C1 C2:
Pentru imaginea completă, trebuie să determinăm coordonatele acestui centru finit al punctului de masă C. Pentru a face acest lucru, trebuie să găsim mai întâi vectorul C1 C2. pentru a ști în ce direcție vor fi deplasate coordonatele punctului C1.
Și acum se calculează coordonatele punctului C
În general, pentru solide centrul de masă și centrul de greutate coincid, bine, sau sunt foarte apropiați unul de celălalt. Iar centrul de gravitate este un astfel de punct al corpului, că dacă puneți suportul corpului în acest moment, acesta va fi în echilibru.
Aceasta incheie lectia noastra de astazi, si aici este temele.
1. Luați în considerare unde magicienii pot aplica cunoștințele acestei lecții.
2. Ce crezi, și cum să găsească centrul de masă al figurii constând din trei trapeze curbe (figura ca suma celor trei trapezoidele curbilinii)?
Trimiteți lucrarea prin Biroul personal
Puteți să vă transferați în siguranță întrebările cu Persephone