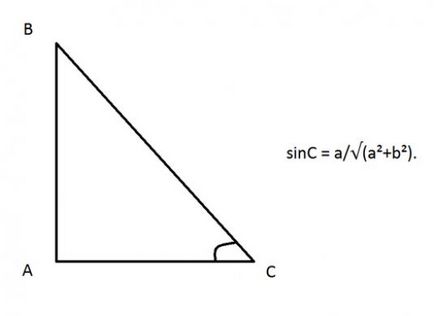
Pentru a găsi sinusul unghiului unui triunghi dreptunghiular, trebuie să ne amintim ce este sinus prin definiție. Și definiția este foarte simplă: sinusul unghiului este egal cu raportul dintre piciorul opus și hypotenuse.
Cum se calculează sines
Dacă avem un triunghi ABC, pentru care A este un unghi drept, atunci laturile AB și AC vor fi picioarele, iar partea BC BC - hypotenuse. Prin urmare, prin definiție, sinusul unghiului B este egal cu raportul piciorului AC la hypotenuse: sinB = AC / BC și sinusul celuilalt unghi sinC = AB / BC.
Într-un triunghi dreptunghiular, funcțiile unghiulare pot fi calculate convenabil: nu sunt necesare construcții suplimentare. Este suficient să cunoașteți lungimea laturilor drepte. Dar, mai des, doar o parte din datele necesare sunt cunoscute, restul ar trebui căutat. Gândiți-vă cum să faceți acest lucru.
Căutând un sinus cu două picioare
Luăm același triunghi ABC cu un unghi drept A, în care știm dimensiunile picioarelor: AB = a, AC = c. Pentru a calcula sinusul unghiului C, este necesar să divizăm cateteza într-o hypotenuse:
Dar hypotenuse va trebui să fie luate în considerare în funcție de teorema lui Pitagora:
Oferim valoarea găsită a hypotenuse (2) în expresie (1), obținem răspunsul:
Căutând un sinez pe hypotenuse și piciorul adiacent
Acum, în același triunghi, trebuie să găsim sinele cu același unghi C, dar știm că hipotensiunea BC = b și catodul AC = c. Cu ajutorul teoremei Pitagora: ABsup2- + ACsup2- = BCsup2- căutați AB:
Acum înlocuiți valoarea găsită a AB în formula pentru sine:
Calcularea sinusurilor pe o parte și un colț ascuțit
În triunghiul ABC cu un unghi drept A, unghiul B = beta- este cunoscut, iar cataloagele AC = c. Trebuie să găsim sinusul unghiului C.
Cel mai simplu - dacă vă amintiți că suma tuturor unghiurilor din triunghi este de 180 °:
Dar puteți merge în altă parte:
Din teorema pitagoreană ABsup2- + ACsup2- = BCsup2- găsim ipoteza:
Substituim valorile cunoscute:
- AB = radic- (csup2- / Sinsup2-beta-csup2-) = radic-csup2- (1 / Sinsup2-beta-1) = cradic- (1 / Sinsup2-beta-1).
Prin urmare, găsim sinusul unghiului C:
- sinC = AB / BC = cradic- (1 / Sinsup2-beta-1) / c / Sinbeta- = Sinbeta- radic- (1 / Sinsup2-beta-1)