Cascada diferențială constă din două etape de amplificare identice cu un OE având un rezistor comun Re în emițători.
Cascada diferențială are două intrări și două ieșiri, precum și două surse de alimentare E1 și E2. incluse în serie.
Principiul cascadei diferențiale se bazează pe simetria sa, care presupune egalitatea rezistențelor în colectorii Rk1 = Rk2 = Rk și identitatea parametrilor tranzistorilor VT1 și VT2.
Să presupunem că cascada diferențială este strict simetrică, iar tensiunile la intrările ei uvx1 = uvx2 = 0. Rezistor Re va avea o tensiune,
unde este tensiunea pe joncțiunile emițătorului cu comutarea directă a tranzistorilor VT1 și VT2.
Prin rezistorul Re va curge un curent direct
Din cauza simetriei circuitului, acești curenți vor curge în circuitul emițătorului, egali cu jumătate din curentul care trece prin rezistorul Re.
În circuitele colectorilor de tranzistori vor curge curenți egali.
Tensiunile la ieșirile cascadei vor fi, de asemenea, egale cu
Deoarece potențialul colectorilor în stadiul diferențial poate varia de la 0 la tensiunea sursei de alimentare E1. apoi pentru a asigura amplitudinea maximă a tensiunii de ieșire de tensiune nedenaturată pe colectorii în starea de repaus ar trebui să fie setată la jumătate din sursa de tensiune E1.
Rezolvând această ecuație în raport cu Rk / Re obținem:
Cel mai adesea (dar nu neapărat) E1 = E2. În acest caz, Rk = Re.
Astfel, în repaus, cascada diferențială este o punte echilibrată. Un braț al podului este format dintr-un tranzistor VT1 și un rezistor RK1. iar celălalt este un tranzistor VT2 și un rezistor Rk2. Pe o diagonală a podului, tensiunea este alimentată de la sursele de alimentare, iar pe cealaltă diagonală tensiunea de ieșire este scoasă.
Datorită simetriei cascadei diferențiale, podul format de acesta va fi echilibrat pentru orice schimbare identică a curenților din umerii podului, indiferent de cauzele care au provocat aceste schimbări.
De exemplu, pe măsură ce crește temperatura, curenții colectorilor vor crește datorită scăderii și creșterii
Acest lucru va duce la o scădere și, totuși, diferența lor va rămâne
Modificarea tensiunii de ieșire a unui amplificator DC în timp sau sub influența factorilor destabilizatori se numește zero drift.
Din raționamentul nostru rezultă că într-o cascadă diferențială perfect simetrică nu există nicio derivație zero.
Aplicăm tensiuni egale ale aceluiași semn la intrările amplificatorului. Astfel de solicitări sunt numite în fază. Lăsați aceste stresuri să fie pozitive. Apoi, curenții emițătorilor și curenții de colector vor crește într-o oarecare măsură. Datorită simetriei circuitului, creșterile curenților colectorului vor fi aceleași și, prin urmare, tensiunea de ieșire va rămâne zero.
Astfel, într-un stadiu diferențial ideal simetric, tensiunile de mod comun nu afectează tensiunea de ieșire.
Oferim intrarea cascadei diferențiale, tensiunea egală în valoare absolută, dar opusă semnului. Astfel de tensiuni se numesc tensiuni diferențiale.
Permiteți concretenței și
Sub influența unui semnal diferențial, curenții colectorilor vor primi incremente egale în valoare absolută și opuse în semnul: ". Potențialul colectorului tranzistorului VT1 va fi incrementat, iar potențialul colector al tranzistorului VT2 este increment
Apoi, tensiunea de ieșire
.
Astfel, o cascadă diferențială ideală simetrică reacționează numai la tensiunea de intrare diferențială, care se reflectă în numele său.
Comparând semnalele tensiunilor și tensiunilor de intrare u, se poate observa că ieșirea 1 inversează în raport cu intrarea 1, iar ieșirea 2 nu este inversată.
Să estimăm parametrii principali ai cascadei diferențiale, pentru care vom face înlocuiri.
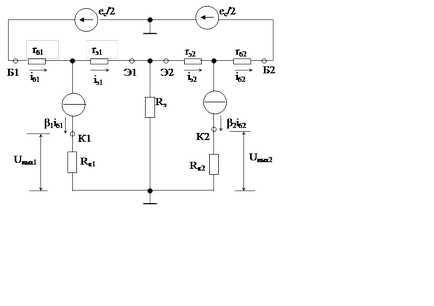
Să găsim impedanța de intrare a fazei diferențiale pentru componenta diferențială a semnalului de intrare.
Să presupunem că între bazele tranzistorilor VT1 și VT2 sursa semnalului este pornită. etc cu. , având o ramură de la mijloc.
Conform celei de-a doua legi a lui Kirchhoff, următoarea ecuație pentru echilibrul de tensiuni pentru conturul format de sursa semnalului de intrare și elementele ,,,
Dar din cauza simetriei circuitului,
Apoi, ținând seama de asta, obținem
Deoarece expresia din paranteze pătrate este impedanța de intrare a cascadei cu AM, se poate concluziona că impedanța de intrare a unei etape diferențial pentru semnalul diferențial este de 2 ori mai mare decât etapa impedanță de intrare cu MA compus din aceleași elemente și care funcționează în același mod
Dacă sursa de semnal este conectată între bazele tranzistorului și punctul său de mijloc este legat la pământ, atunci se consideră că stadiul diferențial are o intrare echilibrată.
Este ușor să se arate că conductorul care leagă punctul intermediar al sursei de semnal la firul obișnuit poate fi îndepărtat.
Într-adevăr, prin acest conductor, curenții bazelor tranzistorilor VT1 și VT2, egali în valoare absolută și opuși în semn, curg, de exemplu, curentul total prin acesta este zero și poate fi scos din circuit fără a perturba distribuția curenților și potențialelor în circuit.
O astfel de intrare, atunci când sursa de semnal este conectată între bazele tranzistorilor și nu are un punct mediu, va fi, de asemenea, simetrică.
Dacă sursa de semnal este conectată între bazele tranzistorilor VT1 și VT2 și una dintre ele este conectată la firul de circuit comun, se spune că treapta diferențială are o intrare asimetrică.
Lăsați semnalul să fie aplicat la baza tranzistorului VT1, iar baza tranzistorului VT2 este conectată la firul comun.
Să estimăm impedanța de intrare a fazei diferențiale pentru un semnal diferențial cu o intrare asimetrică.
În acest caz, impedanța de intrare a etapei diferențiale este o etapă cu impedanța de intrare a EO per tranzistor VT1, care este încorporată în rezistența emițător egală cu rs conectate în paralel și cu impedanța de intrare a cascadei ON tranzistor VT2.
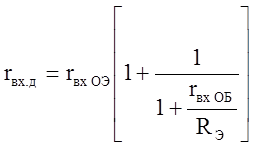
Astfel, dacă impedanța de intrare a treptei diferențiale pentru un semnal diferențial este o intrare simetrică, atunci pentru o intrare asimetrică va fi puțin mai mică.
Diferențele se datorează faptului că, cu o componentă variabilă de tensiune de intrare simetrică a RS rezistor este 0, în timp ce la intrarea dezechilibrată pe RS rezistor va fi o componentă variabilă
În consecință, o componentă variabilă de curent va curge prin rezistența Re
Prin urmare, rezultă că pentru o intrare asimetrică va fi mai puțin cu valoarea curentului, adică, simetria circuitului este încălcată, deși nesemnificativ.