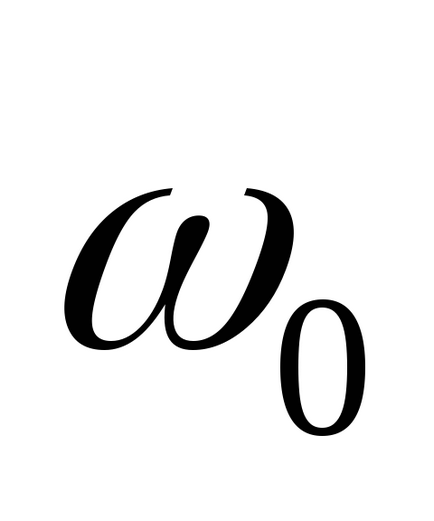Multe dintre proprietățile dinamice ale sistemului (de exemplu viteza, depășirea) sunt determinate de poli ai funcției de transfer (sau, care este același lucru, valorile proprii ale matricei

Funcția de transfer poate fi scrisă ca produs al funcțiilor de transfer a legăturilor elementare ale ordinelor 1 și 2. Astfel, polii funcției de transfer a unui sistem stabil formează poli ai funcțiilor de transfer ale celor două tipuri de legături simple: aperiodice și vibraționale.
O legătură aperiodică cu o funcție de transfer a formei
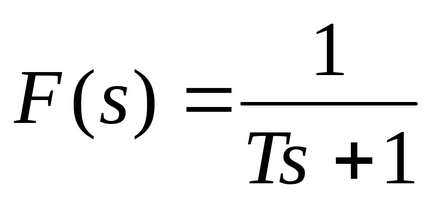
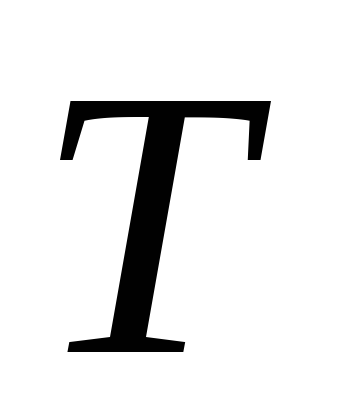
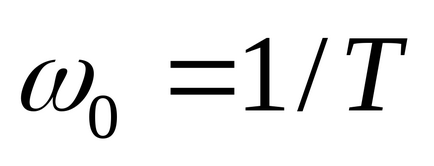
Legătura oscilantă are o funcție de transfer
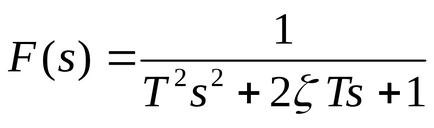
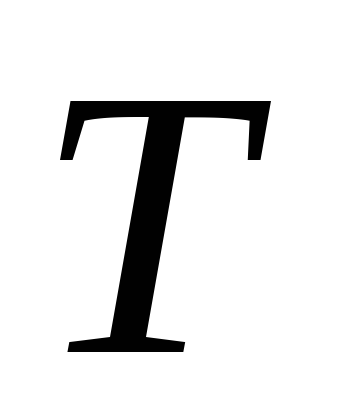
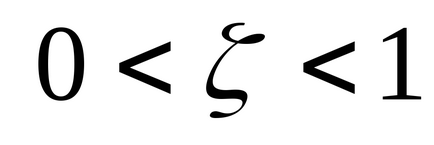
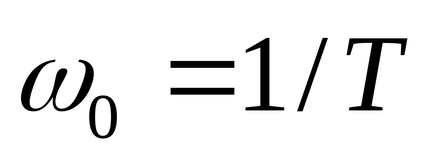


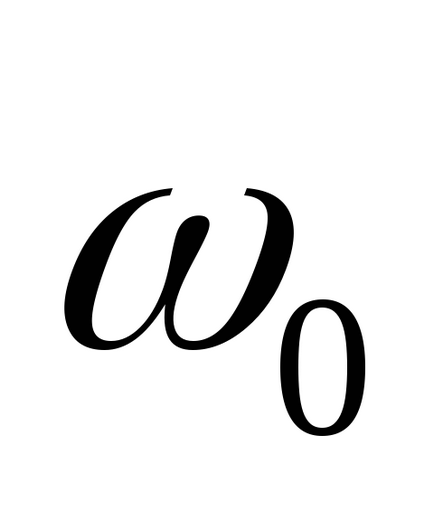
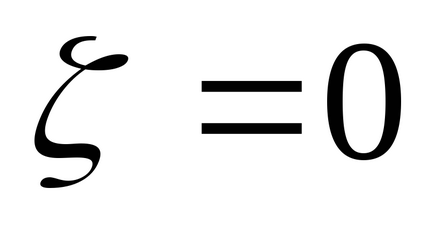
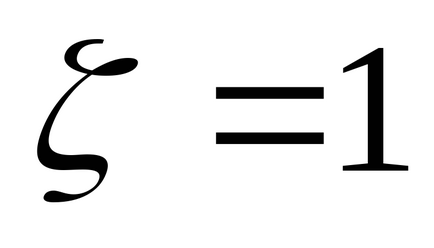
Pentru a găsi polii funcției de transfer f, se poate utiliza funcția
>> [w0, zeta, p] = umed (f)
ne permite să găsim nu numai poli de p. dar și proprietățile eigen corespunzătoare și factorii de amortizare zeta sub formă de matrice.
Zerourile funcției de transfer f sunt calculate ca
Stabilitatea sistemului nu depinde de localizarea zerourilor, dar ele afectează în mod semnificativ procesele tranzitorii. echipă
construiește o hartă a locației zerourilor (acestea sunt notate cu cercuri) și poli (cruci) ale sistemului în planul complex.
1 culoare neagră indică intrarea utilizatorului, albastru - răspunsul mediului Matlab.
2 În literatura de specialitate străină pentru sisteme unidimensionale, se utilizează abrevierea ISO = SingleInputSingleOutput.
3 Polii funcției de transfer sunt valorile proprii ale matricei

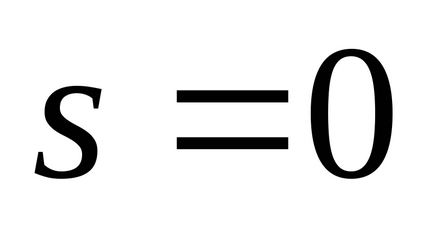

Pentru sistemele neliniare, acest lucru nu este adevărat.
5Znachenie