Atunci când modelul matematic rezultat este complex, adică de nerezolvat, dezvoltatorul recurge la simplificarea sa și la utilizarea unei abstracțiuni mai profunde. În problemele practice de studiere a proceselor de funcționare a sistemelor complexe, procesul invers este deseori de dorit - procesul de extindere a modelului. În același timp, ele încep cu construirea unui model simplu și apoi îl complică. Natura evolutivă a procesului de construire a unui model simplifică rezolvarea problemei ridicate. În primul rând, problemele mai simple sunt rezolvate utilizând un model simplu și apoi sunt stabilite mai multe probleme complexe, ceea ce necesită o potrivire mai consecventă între model și obiectul real, ceea ce duce la un model mai complex.
În ambele cazuri, este necesară simplificarea modelelor matematice ale obiectului.
Cele mai comune sunt următoarele metode pentru simplificarea modelelor:
1) divizarea unui sistem complex într-un număr de subsisteme mai simple (descompunere);
2) identificarea proprietăților și efectelor esențiale și luarea în considerare a celorlalte în formă parametrică (metoda macromodelării);
3) linearizarea proceselor neliniare într-o anumită regiune de variație a variabilelor;
4) reducerea sistemelor cu parametrii distribuiți în sisteme cu parametri lumpedici (introducerea unor ipoteze și limitări mai stricte);
5) neglijarea proprietăților dinamice ale proceselor.
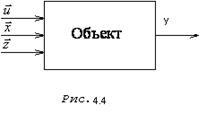
Descompunere. În cazul general, scopul final al descompunerii este partiția spațiului variabilelor obiectului (Fig.4.4) 1. y2. YN. u1. u2. ur. x1. x2. xm. z1. z2. zl> la subspații q cu dimensiuni mai mici, în care se ia în considerare numai conectarea iesirii date yi cu variabilele corespunzătoare. Dacă orice ieșire are o conexiune cu celelalte ieșiri, descompunerea este aproape imposibilă. Dacă modelul general al obiectului are forma unei expresii implicite a unei dimensiuni suficient de mari
și ieșirile yi de la obiect nu au nici o legătură între ele, atunci modelul complex (4.33.) poate fi reprezentat ca un set echivalent cu el n mai multe modele simple simple pentru fiecare ieșire
Datorită descompunerii sistemului, problema cercetării sale teoretice este mult simplificată.
Macromodelling. Când se utilizează metoda macromodelling, numai acelea care afectează variabilele de ieșire sunt lăsate în spațiul variabil inițial (adică, numărate). Efectele unrecorded rămase pot fi luate în considerare în formă parametrică prin modificarea coeficienților variabilelor înregistrate (în cazul efectelor multiplicative) sau prin introducerea unor membri liberi (pentru efectele aditive).
În construirea modelelor simplificate, luând în considerare numai factorii esențiali, metoda de adaptare a modelului este utilizată pe scară largă. și anume modele ale căror coeficienți sunt ajustați astfel încât o anumită măsură de discrepanță (reziduală) a ieșirilor modelului și obiectului să ia valori acceptabile (minime). Pentru aceasta, se utilizează minimizarea reziduurilor. Aceste variabile care se stabilizează și nu duc la o modificare a variabilelor de ieșire nu sunt reflectate în model. Structura modelului simplificat, numit Macromodel poate fi un trei canale cu canalul de control și canalele controlate u x și z impacturi necontrolate, cele două canale și un singur canal (fig. 4.5).
Perturbările în modelele cu două canale și cu un singur canal sunt luate în considerare parametric prin ajustarea coeficienților canalelor rămase.
Model matematic complet
unde sunt vectorii variabilelor controlate și condițiile n1 - vector al coeficienților reglați; - vectori ai variabilelor necontrolate; Luați în considerare, ca exemplu, ideea uneia dintre metodele de adaptare a modelului (metoda de compensare). În Fig.4.6: e = (y - yM) - semnal de neconcordanță între ieșirile obiectului și model; AI - algoritmul de identificare. Algoritmul de identificare vă permite să configurați modelul obiectului după criteriul erorii minime # 949; prin modificarea parametrilor a1 a2. model (ai * valoarea optimă a parametrului ai). Circuitul de mai sus funcționează bine dacă ieșirea este semnalizată fără interferențe. În prezența zgomotului la intrare, se pune problema suprimării interferențelor, care este de obicei rezolvată prin intermediul circuitelor diferențiale care conțin filtre de bandă (metoda diferențială). Liniarizare. Linearizarea modelului original neliniar facilitează rezolvarea unei probleme specifice de cercetare. Prin urmare, pentru a simplifica modelarea și cercetarea, ori de câte ori este posibil, este de dorit înlocuirea ecuației neliniare cu o aproximație liniară, a cărei soluție descrie proprietatea sistemului original neliniar cu o precizie suficientă. Procesul de înlocuire a unui model liniar neliniar se numește linearizare. Dacă neliniar obiectului ecuație diferențială datorită neliniarității caracteristicilor statice, pentru liniarizarea ecuației trebuie să fie înlocuită cu o y caracteristică statică neliniară = F (x) al funcției y liniare = a0 + a1 x. Pentru linearizarea modelului neliniar y = F (x), metoda cea mai general acceptată de deviații mici este cea mai des utilizată. Tehnica construirii ecuațiilor linearizate este în principiu simplă. Substanța matematică a acestei proceduri constă în cerințele față de tipul de neliniaritate a funcției F (x). Pentru a fi liniar, este suficient ca F (x) să existe și să fie continuu într-o vecinătate a unui punct (x0, y0). Apoi liniarizare se realizează prin intermediul unei funcții Taylor serie de expansiune F (x, y), într-o vecinătate a lui (x0. Y0) și îndepărtând toți termenii nelineare ale seriei Indicele 0 înseamnă că derivatele sunt luate la punctul x = x0. y = y0. Astfel, modelul neliniar inițial este înlocuit de un model liniar al formei Aceasta înseamnă că curba y = F (x) este înlocuită de o tangentă în punctul (x0, y0). În cazul unui model multidimensional, adică un model de formă y = F (x1 .x2. Xm), obținem În acest caz, hipersurfele descrise de o funcție neliniară în spațiul variabilelor x1. x2. xm și y, este înlocuită cu un hiperplane tangent la suprafață în punctul (x10.x20.xm0.y0). Este clar că un model linearizat obținut prin extinderea seriei Taylor poate fi adecvat pentru descrierea proceselor dintr-un obiect neliniar care nu sunt legate de variațiile mari ale variabilelor într-un vecin al unui punct. Eroarea de simulare este mai mică, cu atât deviația este mai mică a variabilelor. Să luăm în considerare procesul de linearizare a unui model neliniar prin extinderea lui Taylor în exemplul unui obiect al cărui comportament este descris de o ecuație diferențială neliniară de formă generală F (y ", y ', y, x) = 0. (4.39) Dacă x0. y0 este o stare staționară, atunci coordonatele x și y pot fi scrise în forma x = x0 + Dx, y = y0 + Dy, unde Dx și Dy reprezintă abaterea coordonatelor x și y de la starea de echilibru. Ecuația (4.39) în incremente are forma Descompune partea stângă a ecuației (4.40) într-o serie Taylor în jurul punctului de starea de echilibru (0, 0, y0. X0) și înclinat Dx, Dy și derivații lor de timp sunt mici, vom renunța la toți termenii neliniare ale acestei serii. Aici obținem ecuația care este diferențial liniar cu coeficienți constanți. Ecuația linearizată este de obicei scrisă în următoarea formă: O condiție necesară pentru liniarizare este expansiunea în seria Taylor a funcției F (y ", y ', y, x) într-o vecinătate a punctului corespunzător stării staționare. Ecuația (4.41) înlocuiește aproximativ ecuația (4.39) numai într-o mică vecinătate a punctului (0, 0, y0, x0). Amplitudinea acestei cartiere depinde de forma functiei F (y ", y", y, x), adica a magnitudinilor derivatelor ordonate mai mari decat prima din punctul considerat. În cele mai multe cazuri, folosind modelul linearizat (4.41), se poate studia comportamentul obiectului numai pentru mici deviații ale coordonatelor de intrare și ieșire. Reprezentarea dependenței neliniare inițiale ca o sumă de termeni liniari în expansiunea seriei Taylor presupune o formă cunoscută a acestei dependențe. Numai în acest caz va fi posibil să se calculeze valorile derivatelor. Pentru aceasta, este necesar să se construiască un model neliniar complex și să se scrie formularele într-o formă generală în scopul transformării ulterioare, ceea ce complică procesul de identificare și mărește cantitatea de lucrări computaționale. Este posibilă linearizarea unei funcții neliniare prin intermediul unui plan secant într-un spațiu multidimensional, descris printr-o ecuație liniară coeficienții cărora sunt determinați prin metoda celor mai mici pătrate (OLS), astfel încât să se obțină o bună aproximare a modelului inițial și linearizat într-un anumit interval de posibile modificări ale variabilelor. Aplicarea OLS la calculul coeficienților de linearizare are un efect semnificativ asupra procedurii de construire a ecuațiilor liniare. Cu o astfel de abordare, este suficient să specificăm structura ecuației linearizate, adică să specificăm compoziția variabilelor pe care ar trebui să depindă cantitatea investigată. De aici se poate vedea cu ușurință avantajul aplicării OLS în scopuri de linearizare: nu este întotdeauna posibil să se ofere o formă exactă a unei legături funcționale între variabile într-o formă neliniară. Pentru o abordare statistică, acest lucru nu este necesar, este suficient să nu cunoaștem nici măcar pe toți, ci doar definind în principal variabile pentru a descrie proprietățile unui obiect real. Acest lucru ne permite să abandonăm procedura de construire a ecuațiilor neliniare cu transformarea lor ulterioară, deoarece putem căuta imediat o relație liniară între variabilele obiectului cerute de condiția condiției. Figura 4.7 prezintă geometria a metodelor de linearizare luate în considerare, în care sunt acceptate următoarele notații: a1 este unghiul de înclinare al secantului pe interval # 8710; Dg (linearizarea celor mai mici pătrate); a2 este unghiul de înclinare al tangentei la punctul x = 0 (linearizare prin expansiunea seriei Taylor). Din fig. 4.7 arată clar că folosind OLS a găsit posibilitatea de a evalua intervalul admisibil de liniarizare. Baza pentru aceasta este proprietatea OLS pentru a determina cele mai bune valori ale coeficienților necunoscuți ai modelului linear în domeniul acceptat. 4. Simplificați modelul cu parametrii distribuiți. Caracteristicile stării unui obiect pot depinde nu numai de timp, ci și de coordonatele spațiale. Din setul de obiecte cu parametrii distribuiți, puteți selecta obiecte al căror parametru este redus la unul concentrat. Acestea sunt obiecte pentru care este suficient să cunoaștem valorile variabilelor de intrare și de ieșire într-un număr finit de puncte fixe de spațiu. De exemplu, obiectele liniare cu parametrii distribuiți pot fi reprezentați structural ca un obiect liniar multidimensional cu parametri lumpedi. Apoi, procesele din astfel de obiecte vor fi descrise de un set de modele matematice care determină modificări numai în timpul valorilor de ieșire ale obiectelor la fiecare punct fix din spațiu.Articole similare