Noțiunea de controlabilitate este folosită la verificarea condițiilor de solvabilitate pentru problema sintezei pentru sisteme liniare a căror comportare descrie ecuațiile de stare.
Să luăm în considerare condiția de controllabilitate pentru o clasă generală de obiecte ale formei
Obiectul (6.12) se numește controlat. dacă există o acțiune limitată de control prin intermediul căreia este posibil să se transfere de la starea inițială la un anumit timp finit T într-un timp finit.
Această condiție este verificată utilizând criteriul de controllabilitate, precizăm formularea fără dovezi [1]. Obiectul (6.12) va fi controlat dacă și numai dacă matricea de control
lyaemosti
are rangul maxim.
Deoarece matricea U are n rânduri și coloane, criteriul de controllabilitate este scris în formular
Pentru a determina dacă matricea are un rang întreg, se poate folosi relația
care este ușor de verificat, de exemplu, utilizând pachetul Matlab.
În cazul unui obiect cu un singur canal (când) matricea de control va fi pătrată și criteriul (6.14) va lua forma
Rețineți că problema sintezei va avea o soluție dacă obiectul este controlat, adică Condiția de controlabilitate este o condiție pentru solvabilitatea problemei de sinteză.
Cu toate acestea, neîndeplinirea condiției (6.14) nu înseamnă că un astfel de obiect nu poate fi stabilizat. În cazul în care obiectul (6.12) nu este complet controlat, folosind o transformare specială nondegenerată a variabilelor
descrierea sa poate fi redusă la forma canonică
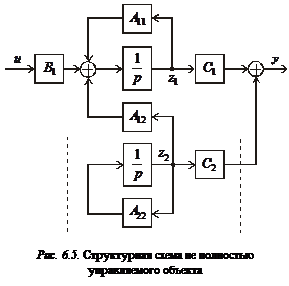
Aici variabilele caracterizează partea autonomă a obiectului, numită neangajată. Schema structurală a unui astfel de obiect este prezentată în Fig. 6.5. Linia punctată identifică partea necontrolată a obiectului, procesele în care se dezvoltă datorită proprietăților proprii. Ele nu pot fi modificate cu ajutorul controlului, dar variabilele afectează partea gestionată și variabilele de ieșire y. Dacă partea neordonată este instabilă, atunci întregul obiect nu va fi numai instabil, ci și instabil.
Astfel, pentru un obiect care nu este complet controlat, condiția pentru solvabilitatea problemei de sinteză este cerința de stabilitate a părții necontrolate.
Verificați controlabilitatea unui obiect al cărui comportament este descris de următorul sistem de ecuații diferențiale:
Să scriem matricea de controllabilitate în formă și să calculam matricile produselor
.
Formăm matricea de control
și de a găsi determinant, prin urmare,
Vom face.