Lăsați o forță externă să acționeze asupra unui arc fără întindere de lungime l 0. extinderea lui cu δl 0 = x 0 (a se vedea figura).
Lăsați o forță exterioară să acționeze asupra unui arc fără întindere cu lungimea l0, întinzându-l la δl0 = x0 (vezi Fig.). La poziția x = x0, Fyp = kx0. După ce forța încetează la punctul x0, arcul este comprimat sub acțiunea forței Fyper.
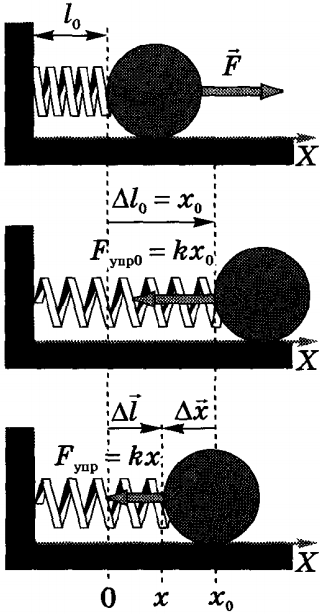
Să determinăm lucrarea forței elastice atunci când coordonatele capătului drept al arcului variază de la x0 la x. Deoarece forța elastică din această secțiune variază liniar, în legea lui Hooke se poate folosi valoarea medie pe această secțiune:
,
Apoi munca (ținând seama de faptul că direcțiile coincid) este egală cu:
.
Se poate arăta că forma ultimei formule nu depinde de unghiul dintre. Lucrarea forțelor elastice depinde numai de deformările arcului în stările inițiale și finale.
Astfel, forța elasticității, ca forța gravitației. este o forță conservatoare.