Definiție 1. Funcția algebrei variabilelor logice este orice funcție a variabilelor n ale căror argumente iau două valori 1 și 0, iar funcția în sine are una din două valori: 1 sau 0.
Fiecare formula algebrică a logicii este o funcție a algebrului logicii. Formula identică, identică și apoi identică, este o funcție constantă.
Se poate arăta că orice funcție a algebrei logice poate fi reprezentată sub forma unei formule de logică și această reprezentare este după cum urmează:
(*)
Formula (*) poate fi transformată într-o formulă care conține numai variabile de expresie elementară și are următoarele proprietăți de perfecțiune (sau proprietăți (C)):
1) fiecare sumă logică a formulei conține toate variabilele care apar în funcție;
2) toate sumele logice ale formulei sunt diferite;
3) nici o summă logică a formulei nu conține aceeași variabilă și negarea ei;
4) nici o summă logică a formulei nu conține aceeași variabilă de două ori.
Folosind tabelul de adevăr care definește funcția, este ușor să obțineți formula corespunzătoare algebricii logice posedând proprietățile (C). Într-adevăr, pentru fiecare set de valori ale variabilelor pe care funcția ia valoarea 1, vom scrie conjuncția variabilelor propoziționale elementare, luând pentru termenul de conjuncție
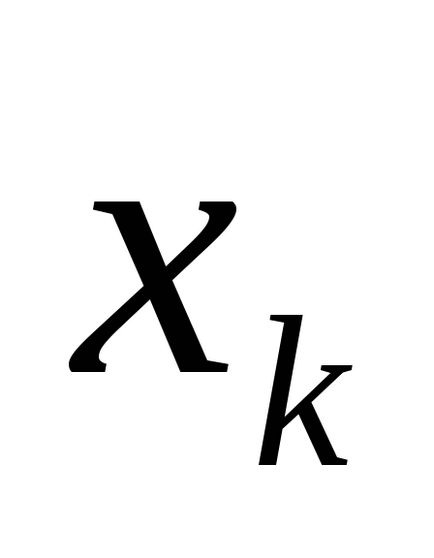
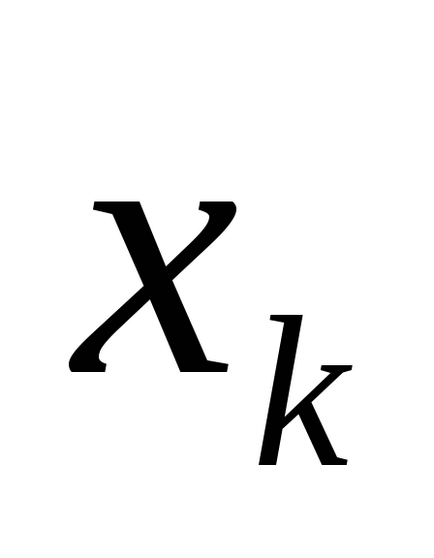
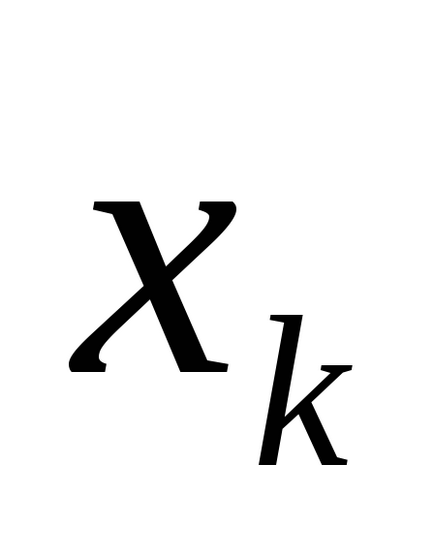
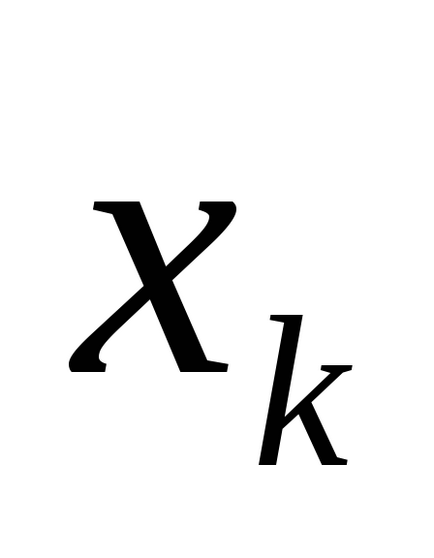
Definiție 2. O conjuncție elementară a variabilelor n este conjuncția variabilelor sau negările lor.
Definiția 3. O formă normală disjunctivă (DNF) cu formula A este o formulă echivalentă cu ea, care este o disjuncție a conjuncțiilor elementare.
Definiția 4. O formă normală disjunctivă perfectă (SDNF) cu formula A se numește DNF A. care posedă proprietățile (C).
CDNF A poate fi obținut în două moduri: a) folosind un tabel de adevăr (vezi mai sus); b) prin transformări echivalente.
Regula pentru obținerea unui CDNF din Formula A utilizând transformări echivalente.
1. Pentru formula A, obținem orice DNF.
2. Din DNP A, prin transformări echivalente, obținem SDNF, obținând succesiv realizarea celor patru proprietăți ale SDNF:
1) Fie B un summand de DNF care nu conține
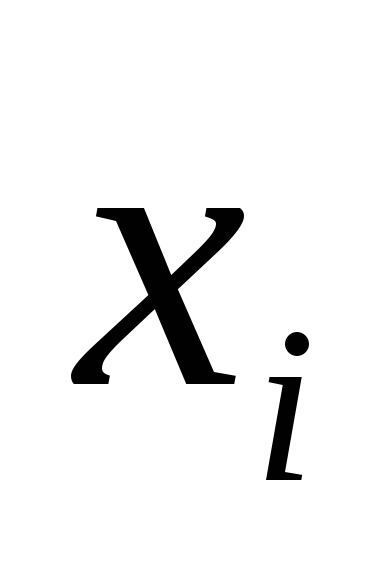
2) Dacă există doi termeni neidentificați în DNP A

3) Dacă într-un anumit termen B în DNP A variabila

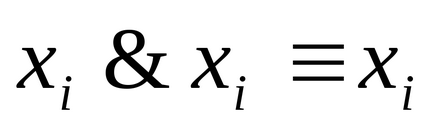
4) Dacă termenul B din DNP A conține o conjuncție
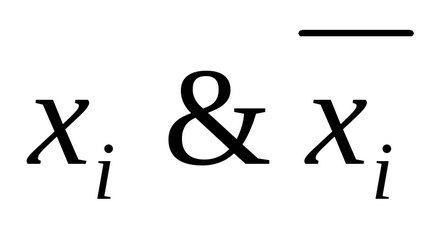
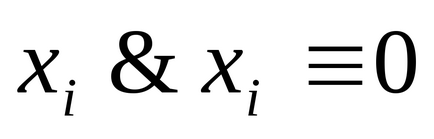
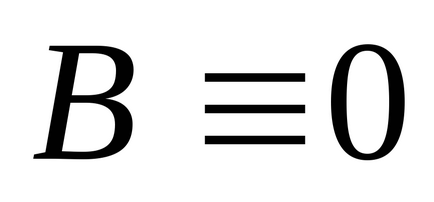
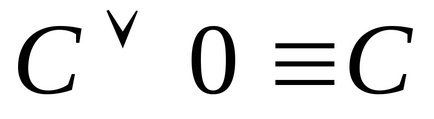
Definiția 5. O disjuncție elementară a variabilelor n este o disjuncție a variabilelor sau negările lor.
Definiția 6. O conjuncție de formă normală (CNF) cu formula A este o formulă echivalentă cu aceasta, care este o combinație de disjuncții elementare.
Definiția 7. O formă normală conjunctivă ideală cu formula A (SKNF A) se numește CNF A. Aceasta satisface patru proprietăți:
1) toate disjuncțiile elementare incluse în CNF A. conțin toate variabilele;
2) toate disjunctiile elementare care fac parte din CNF A. sunt diferite;
3) fiecare disjuncție elementară inclusă în CNF A. conține o singură variabilă;
4) nu o singură disjuncție elementară inclusă în CNF A. conține o variabilă și negarea ei.
SKNF A poate fi obținut în două moduri: a) folosind o tabelă de adevăr (folosind legea dualității, folosim tabelul de adevăr
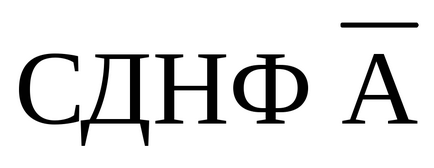
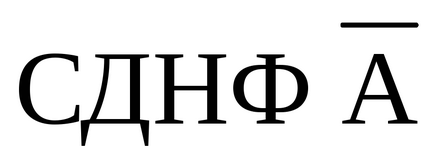
Regula pentru obținerea SKNF de la Formula A utilizând transformări echivalente.
1. Pentru formula A, obținem orice CNF.
2. Din CNF A, prin transformări echivalente, obținem SKNF A. realizând în mod consecvent realizarea a patru proprietăți ale SKNF.
1) Dacă disjuncția elementară B. inclusă în CNF A. nu conține o variabilă
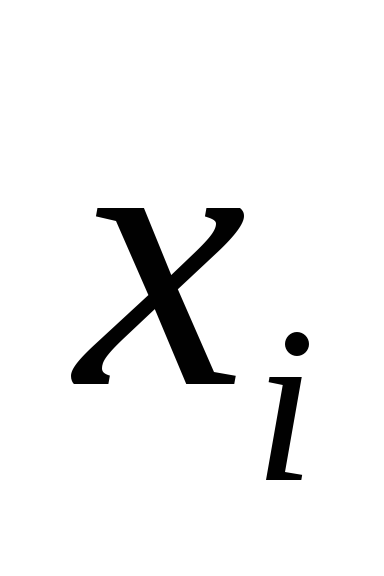
2) Dacă într-o disjuncție elementară B o variabilă
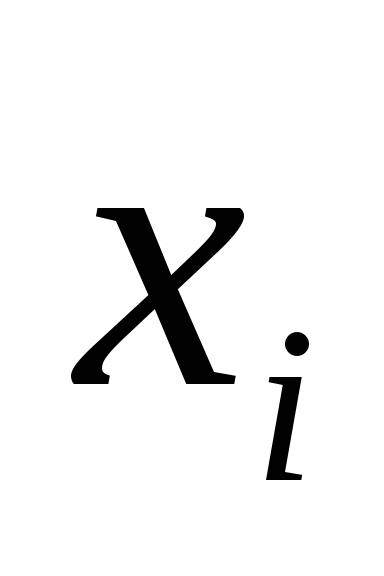
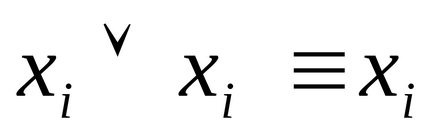
3) Dacă CNF A conține două disjuncții elementare identice, atunci se poate renunța, deoarece
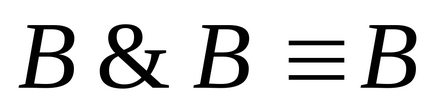
4) Dacă există o pereche în disjuncția elementară
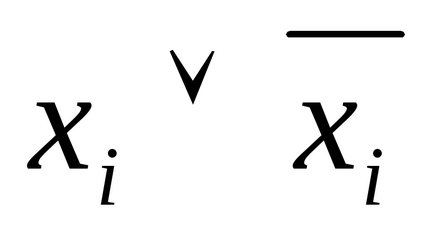
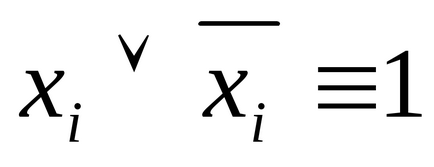
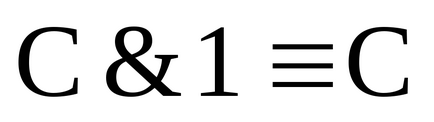
Exemplul 1. Găsiți formula care definește funcția $ (x, y, z) dintr-un tabel de adevăr dat:
Soluția. Folosind regula pentru obținerea unei formule pentru algebra logică din tabelul de adevăr pentru funcția Φ (x, y, z), obținem:
.
Simplificând această formulă, obținem:
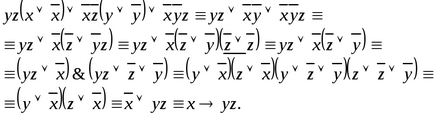
Astfel, se poate presupune formula dorită care definește funcția Φ (x, y, z)
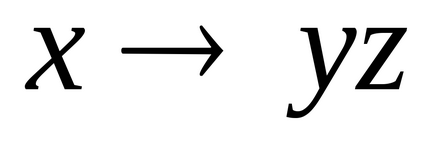
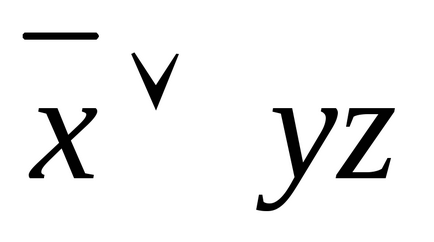
Exemplul 2. Următoarea formulă conduce la SDNF, care a condus-o anterior prin transformări echivalente cu DNF :.
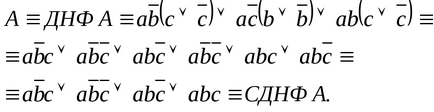
Exemplul 3. Pentru formula din Exemplul 2, găsiți CDNF prin compilarea unui tabel de adevăr.
Soluția. Să compunem tabelul de adevăr pentru formula.
Exemplul 4. Pentru formula din Exemplul 2, găsiți SKNF prin transformări echivalente, care l-au condus anterior la CNF.
Soluția. Din exemplul 2:
.
Exemplul 5. Pentru formula din Exemplul 2, găsiți SKNF scriind DNF înaintea negării sale și apoi utilizând formula dualității.
Toate formulele algebrice ale logicii sunt împărțite în trei clase: 1) identice; 2) identic fals; 3) fezabil.
Formula A este numită satisfăcătoare. dacă ia valoarea 1 pe cel puțin un set de valori ale variabilelor care intră în ea și nu este identic adevărat.
Teorema. Pentru formula algebră a logicii să fie identic adevărată (falsă), este necesar și suficient ca orice disjuncție elementară (conjuncție) care apare în CNF A (DNP A) să conțină o variabilă și negarea ei.
Exemplul 6. Formula va fi identică, identică, falsă sau realizabilă?
Soluția. Să dăm un exemplu într-o formă normală:
Derivarea DNP nu este identică, deoarece fiecare conjuncție elementară nu conține o variabilă și negarea acesteia. Prin urmare, formula originală este identică sau posibilă. Transformăm această formulă la CNF.
Acest produs nu este identic, deoarece suma elementară
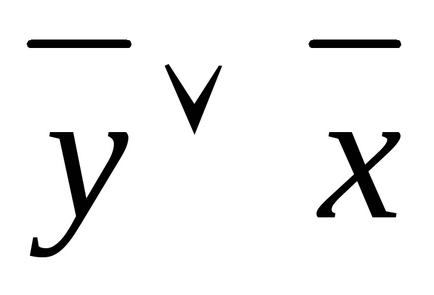
1.34. Folosind tabelul de adevăr, găsiți formulele care definesc funcțiile
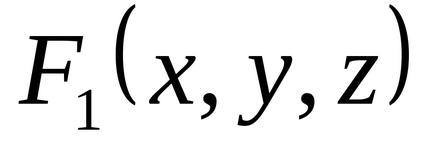
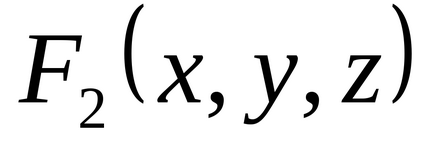
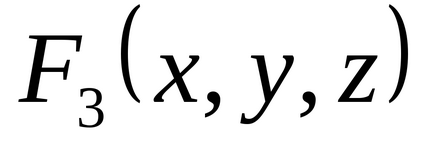
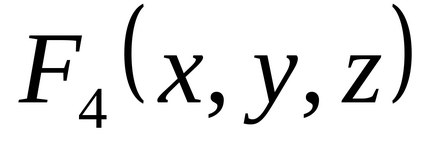
1,35. lăsa
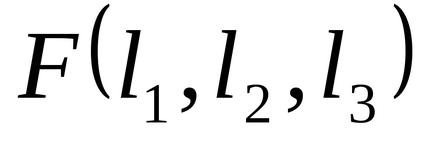
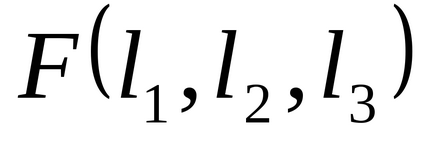
1.36. Noi numim funcția majorității
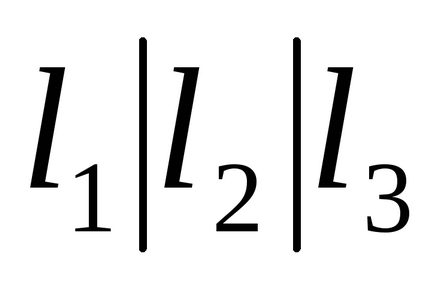
a) Creați un tabel care definește funcția majorității și exprimați această funcție prin operațiile de bază.
b) Simplificați expresia
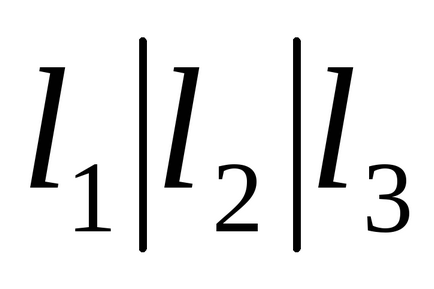
1.37. Funcțiile booleene
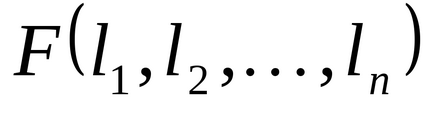
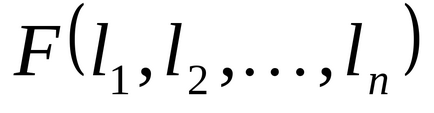
.
Pentru fiecare funcție booleană a două variabile, găsiți funcția booleană duală.
1,38. Funcțiile booleene
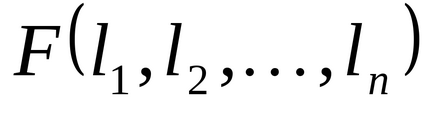
a) păstrarea 0 dacă;
b) păstrarea 1 dacă.
Printre funcțiile booleene a una și două variabile, găsiți toate funcțiile care păstrează 1 și toate funcțiile păstrând 0.
1.39. Pentru formulele următoare, găsiți CDNF și SKNF, fiecare în două moduri (prin egalizarea transformărilor și folosirea tabelelor de adevăr):
1,40. Găsiți CDNF pentru orice formulă identică, care conține: 1) o variabilă, 2) două variabile, 3) trei variabile.
1.41. Găsiți SKNF pentru orice formulă identică, care conține: 1) o variabilă, 2) două variabile, 3) trei variabile.
1.42. Dovediți echivalența formulelor
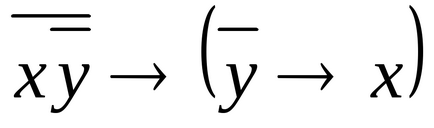
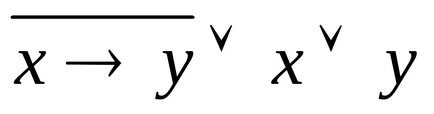
1.43. Găsiți cea mai simplă formă de formule având următoarele forme normale perfecte:
1,44. Folosind criteriul adevărului identic și falsitatea identică a formulei, pentru a stabili dacă formula dată este identică, identică, falsă sau realizabilă: