171 *. Determinați unghiurile pantei drepte AB la pătrat. V și pl. N fis. 166, a).
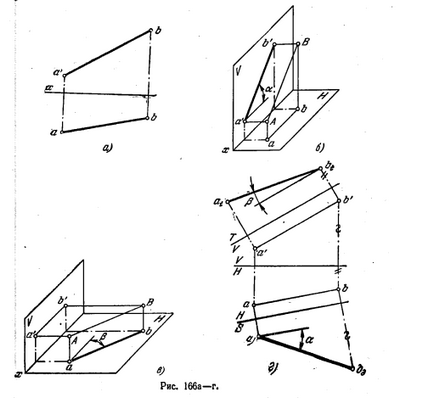
Soluția. Dacă linia este paralelă cu pătratul. V (figura 166, b), apoi unghiul dintre această linie și pătrat. H (unghiul α) este afișat fără distorsiuni față. proiecții. Dacă linia este paralelă cu pătratul. H (figura 166, c), atunci unghiul drept format de acest plan este din Fig. V (unghiul β) este afișat fără distorsiuni la orizont. proiecții. Prin urmare, după ce am setat poziția generală dată prima paralelă cu pătratul. V, și apoi paralel pl. H, putem determina unghiurile a și respectiv β.
În Fig. 166, d arată aplicarea metodei de schimbare a pl. proiecții pentru a determina unghiurile α și β. Deci, pentru a determina unghiul α, un pl suplimentar. S, perpendicular pe pătrat. H și paralel AB și pentru determinarea unghiului β - un plan suplimentar T ⊥ V și în același timp || AB.
În Fig. 166, d drept în timp ce se rotește: a) în jurul axei care trece prin punctul B și perpendicular pe pătrat. H, înainte de paralelismul pieței. V (poziția a'1 b ', a1 b) -
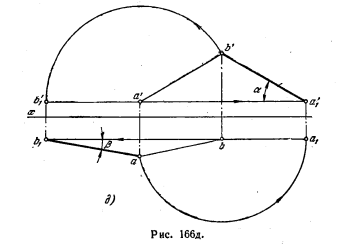
unghiul α este determinat; b) în jurul unei axe care trece prin punctul A perpendicular și pl. V, paralel cu pătratul. H (poziția a'b'1, Ab1) - unghiul β este definit.
Desigur, puteți desena aceste axe pe desen; dar, aparent, construcția este posibilă fără acest lucru.
172. Piramida SABCD este dată (vezi Figura 154). Determinați unghiurile de înclinare a marginilor piramidei către pătrat. V și pl. N.
173 *. Determinați unghiul pantei planului dat triunghiurilor ABC (fig.167, a) la pătrat. H și pl. V.
Soluția. După cum se știe, unghiul de înclinare (α) al planului la pătrat. H este proiectat fără distorsiuni pe pătrat. V dacă planul este perpendicular pe pătrat. V (figurile 167, 6) și unghiul de înclinare (β) al planului spre pătrat. V este proiectat fără distorsiuni pe pătrat. H, dacă planul este perpendicular pe pătrat. H (fig.167, c).
În Fig. 167, r, pentru a determina unghiurile, trecem la sistemul S, H, unde n. S este perpendicular pe pătrat. H și la un plan dat (axa S / H este perpendiculară pe orizontul proieciei a-1 a orizontalei).
Determinarea unghiului β a fost efectuată trecând de la sistemul V, H la sistemul T, V, unde n. T este perpendicular pe pătrat. V și la planul dat al triunghiului (axa T / V este perpendiculară pe partea frontală a proiecției c'2 'a frontului).
În Fig. 167, d, aceeași problemă este rezolvată prin metoda deplasării paralele. Mai întâi, toate vârfurile triunghiului dat ABC sunt deplasate în planuri paralele cu H, astfel încât planul triunghiului este perpendicular pe plan. V. Acest lucru
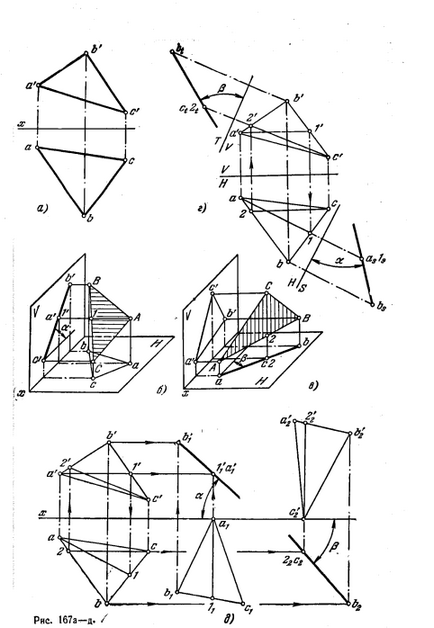
este atins cu ajutorul A-1 orizontal, mutat astfel încât să fie situat perpendicular pe pătrat. V (proiecția orizontală a1 este perpendiculară pe axa x). Obținem unghiul α al înclinării planului triunghiului către pătrat. H fără distorsiuni.
Pentru a determina unghiul β al pantei planului triunghiului ABC la pătrat. Triunghiul este rotit astfel încât să fie perpendicular pe pătrat. H. Aceasta se face cu ajutorul frontalului C-2: este perpendicular pe pătrat. H (poziția C2 22. proiecția frontală c'2 2'2 ⊥ x) și, prin urmare, planul care trece prin această față este, de asemenea, perpendicular pe plan. H.
174. Piramida SABC este dată (vezi Figura 161). Determinați unghiurile de pante ale fețelor SAB, SAC și ABC la pătrat. H și pl. V.
175. Este dat un paralelipiped (vezi Figura 165). Determinați unghiurile pantei bazei ABCD și a feței CDHG în pătrat. V și se confruntă cu ADEH la pl. N.
176 *. Determinați magnitudinea unghiului BAC (figura 168, a).
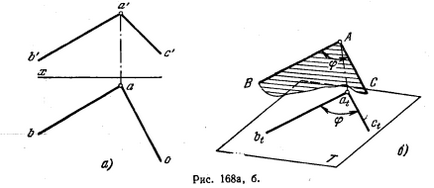
Soluția. Dacă planul unghiului este paralel cu un pătrat. proiecțiile, atunci acest unghi este proiectat pe el fără distorsiuni (figura 168, b).
În Fig. 168, problema este rezolvată prin metoda de schimbare a patratului. proiecții. Deoarece planul unghiului BAC este un plan de poziție generală (orizontul său nu este perpendicular pe niciuna dintre planele V, H, W), este mai întâi necesar să se completeze sistemul V, H m. S, luând-o perpendicular pe pătrat. H și la planul unghiului BAC. Ca urmare a acestei transformări, proiecția unghiului pe planul S este obținută ca un segment ca ls. Acum puteți introduce un pătrat suplimentar. (T), trecând-o perpendicular pe pătrat. S și în același timp paralel cu planul unghiului BAC. Unghiul lt la 2t reprezintă valoarea reală a unghiului BAC.
În Fig. 168, iar unghiul necesar φ este determinat prin metoda deplasării paralele.
Mai întâi, planul unghiului este mutat astfel încât să devină perpendicular pe pătrat. V (pentru aceasta avem proiecția orizontală orizontală perpendiculară pe axa x). Apoi avem planul unghiului paralel cu pătratul. H, pentru care mutăm proiecția 1'1 a'1 în poziția 1'2 a'2 (adică, axa x). O altă construcție este prezentată în Fig. 168,6. Pentru a determina unghiul, se aplică o rotație în jurul orizontală: planul unghiului va fi paralel cu pătratul. H (poziția T).
Construcțiile sunt realizate în următoarea ordine:
1. Planul de rotație al punctului A este un plan orizontal proiectat. R, perpendicular pe orizontală (adică pe axa de rotație).
2. Centrul de rotație al punctului AB este marcat de intersecția orizontală cu pătratul. R (punctul O, O ') și proiecțiile razei de rotație (Oa și O'a') sunt indicate.
3. Se determină valoarea naturală a razei de rotație (se exprimă prin hypotenuse OA a triunghiului Oa A).
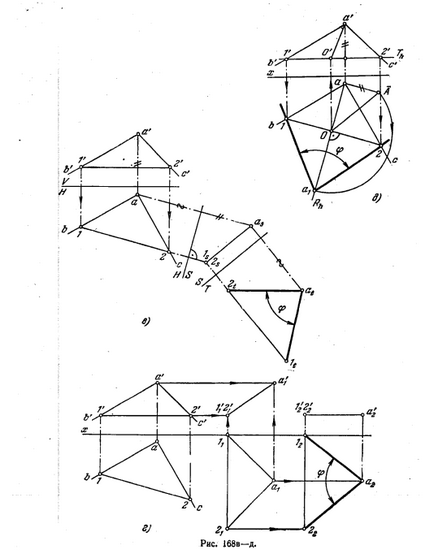
4. Se întocmește un arc cu un rază de 0 A pe Rh. a1 este orizontul. proiecția vârfului unghiului după rotirea sa în jurul orizontului până la alinierea cu pătratul. T - și unghiul 1a1 2 este construit, care este egal cu cel dorit.
Pentru rezolvarea problemelor de tipul 176, cea mai rațională este aplicarea rotației în jurul orizontului (sau frontal), așa cum se arată în Fig. 168, d.
177. Piramida SABC este dată (vezi Figura 156). Rotiți în jurul orizontului pentru a determina unghiul dintre coaste și SB, SB și SC, SC și SA.
178. Având un paralelipiped (vezi Figura 165). Determinați unghiurile dintre marginile DH și CD, CG și CD, AB și BC.
179 *. Determinați valoarea unghiului dintre liniile încrucișate AB și CD (figura 169, a).
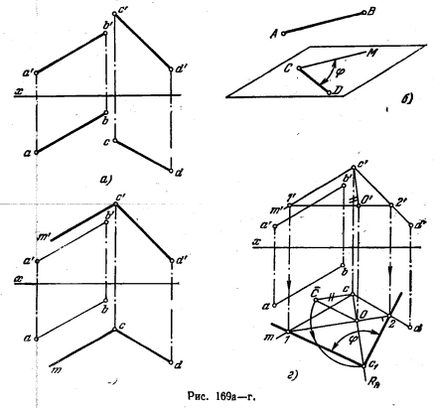
Soluția. Unghiul dintre două linii încrucișate este determinat de unghiul obținut de liniile intersectate, respectiv paralel cu datele traversate. Pentru a determina valoarea unghiului, începeți cu imaginea pe desen. Acest lucru se face în Fig. 169,6, utilizând una din liniile drepte date - CD, prin punctul C a căruia o linie dreaptă CM este trasată paralelă cu o altă linie dată - AB. Mărimea unghiului MCD (figura 186, c) exprimă unghiul dintre liniile AB și CD. Aceasta se face prin întoarcerea în jurul orizontală 1-2 (Figura 169, a), luată în pl. unghi MCD.
180. Piramida SABC este dată (vezi Figura 160). Determinați valoarea unghiului dintre marginile sale: a) SB și AC, b) SA și BC.
181 *. Determinați unghiul φ al pantei liniei drepte AB în planul definit de triunghiul CDE (figura 170, a).
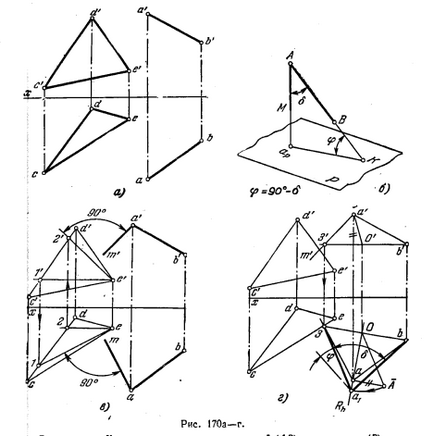
Soluția. După cum se știe, unghiul dintre linia dreaptă (AB) și planul (P) este un unghi ascuțit (φ) între linie și proiecția acesteia (AP K), pe acest plan. Pentru a construi (Fig.170b) acest unghi, este necesar să găsim punctele de intersecție cu pl. P liniei AB și perpendicularul tras din orice punct al liniei AB pe pătrat. P. Dar, în cazul în care, la fel ca în această problemă, este necesar doar pentru a determina unghiul de înclinare față de planul liniei, este mai ușor să se determine magnitudinea unghiului δ, suplimentar la cp unghiul: găsirea ö unghi, se poate determina unghiul φ din relația φ = 90 ° - δ. În Fig. 170 ilustrează structura unei am proiecție și a'm „perpendicular pe planul triunghiului CDE, care sunt luate tsfrontal acest plan orizontal: am ⊥ e - 1, a'm“ ⊥ e2“.
Acum putem determina (figura 170, d) valoarea naturală a unghiului δ cu vârful A, care se face prin întoarcerea în jurul orizontului b'Z ', b-3. Unghiul dorit este φ = 90 ° -δ.
182. Piramida SABC este dată (vezi Figura 1611. Determinați unghiurile pantei marginilor SA, SB și SC pe fața ABC
183 *. Determinați unghiul dintre fețele ABC și ABD (fig.171, a).
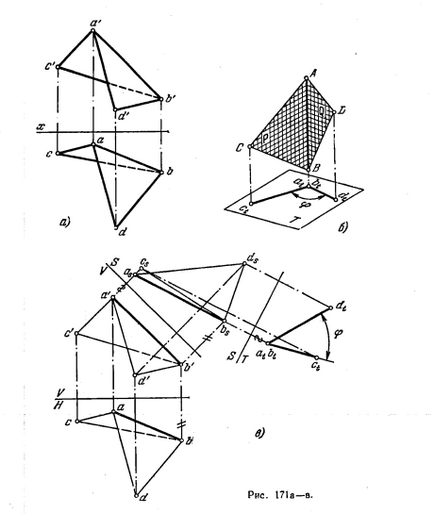
Soluția. Unghiul diedru este măsurat unghiul liniar obținut la intersecția dintre fețele planului unghiului diedru perpendicular pe ambele fețele diedrului, și în consecință, la linia de intersecție, t. E. Marginea unghiului diedru. Dacă această margine AB este perpendiculară pe orice pătrat. T (figura 171.6), apoi valoarea obținută pe pătrat. Proiecția unghiului dihedral exprima unghiul liniar.
Pentru a rezolva problema (Fig.171, c), se aplică metoda de schimbare a pătratului. proiecții. Din sistemul V, H se completează trecerea la sistemul S, V, unde S ⊥ V și S || AB, iar apoi de la acest sistem trecerea S, V la sistemul T, S, unde T ⊥ S și T ⊥ AB.
Triunghiurile sunt proiectate pe un pătrat T în formă de segmente la ct și la dt. Unghiul dintre ele este egal cu unghiul dorit φ.

În Fig. 171, d prezintă soluția aceleiași probleme cu ajutorul metodei de deplasare paralelă: marginea AB este plasată perpendicular pe pătrat. N.
184 *. Determinați valoarea unghiului format de planul P și planul triunghiului ABC (figura 172, a).
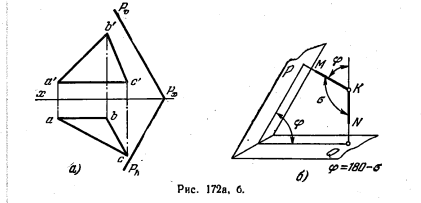
Soluția. Dacă, în rezolvarea acestei probleme, aderă la schema de soluții a celei anterioare, este necesar să construim o linie dreaptă de intersecție a planurilor date. Dar se poate face altfel, fără a construi această linie, adică fără a determina marginile unghiului dorit dorit. Putem proceda după cum urmează: nu este direct să determinăm unghiul φ, ci unghiul σ (figura 172, b) între perpendicularii KM și KN trase de la un anumit punct K la planurile date. După ce am găsit unghiul σ, obținem φ = 180 ° - σ.
O astfel de soluție diferă în esență de soluțiile din Fig. 171, în și 171 și. Luând un punct K (figura 172, c), tragem din acesta perpendiculele KN și KM, respectiv, pe planul triunghiului ABC și pe plan. P: din punctul k 'tragem k'n' ⊥ a'b 'și k'm' ⊥ Pϑ. și din punctul k - kn ⊥ ac și km ⊥ Ph. Astfel, un unghi cu proiecțiile mkn și n'k'n '(unghiul σ) este obținut. Valoarea naturală a acestui unghi este obținută prin rotirea frontului 1-2 (figura 172, d). Deoarece se obține un unghi ascuțit,
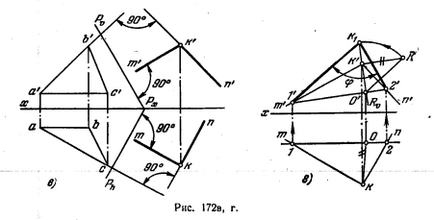
presupune că determină unghiul necesar între planurile date, deoarece din unghiurile adiacente obținute prin intersecția celor două planuri, unghiul dintre planuri este considerat a fi acut.
185. Se dă piramida SABCD (vezi Figura 154). Determinați unghiurile dintre fețele SAB și SBC, SBC și SCD, SAD și SAB prin metoda de schimbare a planurilor de proiecție.
186. Este dat un paralelipiped (Figura 165). Determinați unghiurile dintre fețele CDHG și EFGH, BCGF și CDHG.