Simetria cristalelor .......................................................... 8
Simetria spațiului ...................................................... 14
Simetria timpului ............................................................ 15
Simetria este o astfel de caracteristică a naturii, despre care se obișnuiește să spunem că acoperă toate formele de mișcare și organizare a materiei. Originile conceptului de simetrie revin anticilor. Cea mai importantă descoperire a anticilor a fost realizarea asemănării și a diferenței dintre dreapta și stânga. Aici, propriul corp, precum și corpurile animalelor, păsărilor și peștilor au servit ca specimene naturale.
Iată ce a scris cercetătorul rus, om de știință al depozitului din Lomonosov, enciclopedist al VI-lea. Vernadsky în lucrarea sa „Compoziția chimică a biosferei Pământului și mediul său“:“... un sentiment de simetrie și o dorință reală de a exprima in casa si nu a existat viață în omenirea de unelte de piatră Paleolitic sau chiar, adică perioadele cele mai lungi din preistoria omenirii, care au durat Paleoliticul este de aproximativ o jumătate de milion de ani, iar pentru eolit - milioane de ani. Acest sentiment și lucrarea legată de el, care încă se schimbă brusc și intens, au afectat neoliticul cu 25.000 de ani în urmă ".
De asemenea, vă puteți aminti monumentele magnifice ale vechiului antichitate, unde se manifestă în mod deosebit vii. Acestea sunt templele vechiului Babilon și piramidele din Giza, palatul din Ashur. Deci, din moment ce cele mai vechi timpuri, din moment ce, aparent cu Neoliticul, oamenii au realizat treptat și a încercat să-și exprime în imagini faptul că, în natură, cu excepția distribuției aleatorie a obiectelor identice sau părți ale acestora, există anumite modele spațiale. Ele pot fi destul de simple - repetarea consecventă a unui obiect, mai complexă - întoarcerea sau reflexia în oglindă. Pentru a exprima cu exactitate aceste modele, au fost necesare condiții speciale. Potrivit legendei, Pythagoras Regiysky a venit cu ei.
Termenul „simetrie“, ceea ce înseamnă literalmente proporționalitatea (proporțională, uniformitate, armonie), Pitagora Regiysky desemnată regularitate spațială în aranjamentul figurilor părți sau piese identice în sine. Simetria se poate manifesta în mișcări, curbe sau reflexii în oglindă.
Simetria - din simetria greacă, ceea ce înseamnă proporționalitate - reflectă interdependențele universale ale obiectelor lumii, exprimate simultan în raportul identității și diferenței lor.
Originile ideilor de simetrie cu rădăcinile lor profunde se îndreaptă către lumea spirituală a popoarelor din Anticul Antic, Grecia și Roma.
Una dintre descoperirile importante ale științei naturale moderne este faptul că întreaga diversitate a lumii fizice care ne înconjoară este asociată cu această încălcare a anumitor tipuri de simetrii. Pentru a face această afirmație mai ușor de înțeles, să luăm în considerare conceptul de simetrie în detaliu. "Simetricul se referă la ceva care are o bună proporție de proporții, iar simetria este acea consistență a părților individuale care îi unește într-un întreg. Frumusețea este strâns legată de simetrie ", a scris H. Weil în cartea sa" Studii de simetrie ". El se referă aici nu numai la relațiile spațiale, adică geometrie simetrie. Un fel de simetrie, el consideră armonia în muzică, indicând aplicațiile acustice ale simetriei.
Oglinda simetrie în geometrie se referă la operațiunile de reflexie sau de rotație. Este destul de răspândită în natură. Cristalele au cea mai mare simetrie în natură (de exemplu, simetria fulgilor de zăpadă, cristalele naturale), dar nu toate au o simetrie oglindă. Sunt cunoscute așa-numitele cristale optic active care rotesc planul de polarizare a luminii care se află pe ele. În cazul general, simetria exprimă gradul de ordonare a oricărui sistem sau obiect. De exemplu, cercul este mai ordonat și, în consecință, simetric decât pătratul. La rândul său, pătratul este mai simetric decât dreptunghiul. Cu alte cuvinte, simetria este invarianța (invarianța) oricăror proprietăți și caracteristici ale unui obiect cu privire la orice transformări (operații) asupra acestuia. De exemplu, cercul este simetric față de orice linie (axa simetriei) situată în planul său și care trece prin centru, este simetrică și relativă față de centru. Operațiile de simetrie sunt în acest caz oglindă reflectorizantă față de axă și rotație față de centrul cercului.
Într-un sens larg, simetria este un concept care reflectă ordinea existentă în realitatea obiectivă, o anumită stare de echilibru, stabilitatea relativă, proporționalitatea și proporționalitatea între părți ale întregului. Conceptul opus este acela de asimetrie, care reflectă esența lumii obiective în încălcarea ordinului, echilibrul, stabilitatea relativă a proporționalității și proporționalitatea între părțile individuale ale unui întreg, ca urmare a schimbării, dezvoltarea și restructurarea organizațională. Deja acest lucru implică faptul că asimetria poate fi văzută ca o sursă de dezvoltare, evoluție, formarea de noi. Simetria poate fi nu numai geometrică. Distingem formele geometrice și dinamice de simetrie (și, prin urmare, asimetrie). Forma geometrică a simetriei (simetria exterioară) include proprietățile spațiului-timp, cum ar fi omogenitatea spațiului și a timpului, izotropia spațiului, echivalența cadrelor de referință inerțiale și așa mai departe.
Simetria se referă la forma dinamică. exprimând proprietățile interacțiunilor fizice, de exemplu, simetria încărcăturii electrice, simetria rotației și așa mai departe. (simetrie internă). Fizica moderna, cu toate acestea, releva posibilitatea de a reduce toate simetriile la simetrii geometrice.
Spre deosebire de artă sau tehnologie, frumusețea în natură nu este creată, ci doar fixă, exprimată. Printre varietatea infinită de forme de viață și de natură neînsuflețită, imagini atât de perfecte se întâlnesc în abundență, a căror apariție ne atrage atenția în mod invariabil. Astfel de cristale includ unele cristale, multe plante.
În simetria conformă (circulară), transformarea principală este inversarea în raport cu sfera. Pentru simplitate, vom lua un cerc cu raza R centrată la O. Inversiunea acestui cerc este definit ca o transformare de simetrie, care transformă orice punct P la un punct P“, care se află pe prelungirea razei care trece prin punctul P la o anumită distanță de centrul:
Simetria conformă are o mare generalizare. Toate transformările cunoscute de simetrie: reflexiile oglinzilor, rotațiile, deplasările paralele sunt doar cazuri speciale de simetrie conformă.
Principala caracteristică a transformării conformale este aceea că păstrează întotdeauna unghiurile figurinei și sferei și intră mereu în sfera unei alte raze.
Se știe că cristalele unei substanțe pot avea multe forme diferite, dar unghiurile dintre fețe sunt întotdeauna constante.
Oglinda simetrie. Este ușor de stabilit că fiecare figură simetrică plană poate fi combinată cu ea însăși prin intermediul unei oglinzi. Este surprinzător faptul că figuri complexe, cum ar fi o stea cu cinci puncte sau un pentagon echilateral, sunt de asemenea simetrice. După cum rezultă din numărul de axe, acestea diferă precis prin simetrie înaltă. Și invers: nu este atât de ușor de înțeles de ce o figură aparent corectă, ca paralelogramul oblic, este asimetrică. La început, se pare că paralel cu una din laturile sale ar putea trece axa simetriei. Dar merită să încercați din punct de vedere mental să o utilizați, de îndată ce sunteți convins că nu este așa. Spirala este, de asemenea, asimetrică.
În timp ce cifrele simetrice respectă pe deplin reflexia lui, asimetric diferit de acesta: de la șurubul de spirala de la dreapta la stânga, în oglindă va transforma spirala, de spin de la stânga la dreapta.
Dacă puneți literele în fața oglinzii, plasându-le paralel cu linia, veți observa că aceia dintre aceștia ale căror axă de simetrie trece orizontal pot fi, de asemenea, citite în oglindă. Dar cei ale caror axe sunt verticale sau absente la toate, devin "necitite".
Există limbi în care semnul semnelor se bazează pe prezența simetriei. Deci, în scrisul chinezesc, hierogliful înseamnă exact mijlocul adevărat.
În arhitectură, axele de simetrie sunt folosite ca mijloc de exprimare a unui design arhitectural. În tehnică, axa de simetrie este indicată cel mai clar acolo unde este necesară estimarea deviației de la poziția zero, de exemplu, pe volanul unui camion sau pe volanul unei nave.
Simetria se manifestă prin diferitele structuri și fenomene ale lumii anorganice și ale naturii vii. În lumea naturii neînsuflețite, farmecul simetriei este făcut de cristale. Fiecare fulg de zăpadă este un mic cristal de apă înghețată. Forma fulgilor de zăpadă poate fi foarte diversă, dar toate au simetrie - simetrie rotativă a ordinii a șasea și, în plus, o simetrie în oglindă.
Simetria similara. În spațiu, există corpuri care au simetrie elicoidală; Combinată cu poziția sa inițială după ce a fost transformată într-un unghi în jurul axei, suplimentată de o deplasare de-a lungul aceleiași axe. Dacă un unghi dat este împărțit la 360 de grade este un număr rațional, atunci axa rotativă este și axa de transfer.
Corpurile solide ale naturii există în două forme: amorfă și cristalină. Corpurile amorfe sunt reprezentate de ochelari, rășini, materiale plastice, var, bitum, ceară etc., de asemenea, pot fi atribuite acestora. Corpurile cristaline sunt cele mai multe corpuri ale naturii - nisipurile, argilele, bazalturile, granitele, metalele, majoritatea mineralelor naturale și compușii chimici. Unele dintre ele pot exista sub formă de cristale unice - de corpuri cu fațete regulate geometric (roca de sare, cristal de rocă, sulfat de cupru, etc.), o semnificativă minerale porțiune natură - corpul policristalin.
Rezultatele studiilor arată că structura corpurilor amorfe și a lichidelor se află în așa-numita ordine cu rază scurtă de acțiune. Aranjamentul particulelor corpului dezvăluie o anumită tendință de a ordona, în timp ce structura corpurilor cristaline se datorează prezenței unei ordini pe termen lung. Aranjamentul particulelor corpului este comandat geometric în întregul volum. Este obișnuit să o afișăm folosind un model geometric - o latură de cristal.
O examinare a structurii cristaline a solidelor ne convinge că este posibil să selectăm în mod arbitrar un anumit volum mai mic (celula unică), prin traduceri paralele din care se poate obține întregul cristal. Astfel, plasăm simetria translațională în primul rând în structura corpurilor cristaline.
De exemplu, luați în considerare o celulă elementară simplă (a se vedea figura 4.2). Se determină prin trei vectori a, b, c ai traducerilor elementare și trei unghiuri a. b. g.
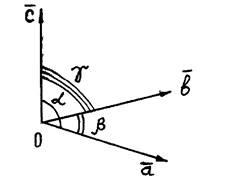
Figura 4.2. Definirea unei celule unitate
Alte proprietăți de simetrie ale cristalelor sunt afișate utilizând așa-numita latură Bravais.
Lattica Bravais dezvăluie elementele caracteristice ale simetriei în aranjarea atomilor identici și localizați în mod identic. Această imagine geometrică caracterizează simetria cristalelor în ceea ce privește funcționarea simetriei oglinzii, axiale, centrale, oglindă-rotație a oglinzilor. Trebuie avut în vedere faptul că adesea elementul celular este reprezentat nu de o singură latură Bravais, ci de o suprapunere de două sau mai multe. Mai jos (Fig.4.3-4.9) sunt prezentate toate tipurile posibile de laturi Bravais. Se pare că pot fi mulți. Totuși, acest lucru nu este cazul. Ideea este că toate operațiile de simetrie trebuie să fie compatibile cu funcționarea simetriei translaționale, iar această circumstanță reduce în mod esențial numărul de laturi posibile, limitându-le numărul la 14 tipuri, unite în 7 grupuri spațiale (syngony).
Cea mai importantă este faptul că în cristale, simetrii rotației din ordinul al cincilea sunt excluse și, de asemenea, simetriile de rotație ale ordinului mai mari decât cea de-a șasea. Eliminarea simetriei ordinii a cincea (pentagonală) reprezintă un fapt remarcabil de natură, pe care o vom discuta mai târziu.
O consecință a simetriei cristalelor este anizotropia proprietăților lor, cu alte cuvinte, asimetria lor față de direcțiile diferite ale cristalului. Prin urmare, toate proprietățile cristalelor ar trebui împărțite în scalar, care nu depind de alegerea direcției și de vectori. Capacitatea termică, punctul de topire, temperatura de topire etc .; la a doua - conductivitate electrică, conductivitate termică, proprietăți mecanice, optice, magnetice. Vedem că simetria este strâns legată de asimetrie. Organismele care sunt mai asimetrice într-o proprietate fizică se pot dovedi a fi mai simetrice în cealaltă.
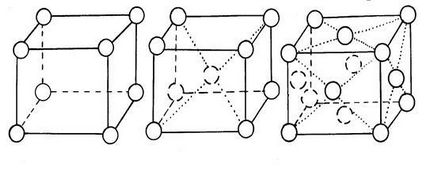
a) simplu; b) centru centrat (bcc);