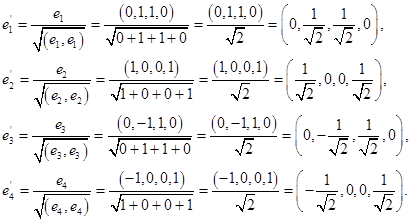Să găsim vectorii proprii ai unui operator liniar dat.
Un număr este o valoare proprie a operatorului dacă și numai dacă. Notăm ecuația caracteristică:
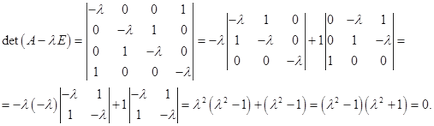
Rezolvăm, avem
Astfel, obținem valorile proprii ale operatorului:
Pentru fiecare dintre valorile proprii obținute, găsim vectorii proprii.
Ele pot fi găsite de sistemele lor.
Rezolvăm sistemul omogen de ecuații.
Matricea coeficienților are gradul 2. Noi alegem ca minori de bază Apoi, presupunând că avem
Astfel, soluția generală a sistemului
.
Din soluția generală găsim un sistem fundamental de soluții:
.
Cu ajutorul unui sistem fundamental de soluții, soluția generală poate fi scrisă în formă.
Rezolvăm sistemul omogen de ecuații
.
Matricea coeficienților are gradul 2. Noi alegem ca minori de bază Apoi, presupunând că avem
Astfel, soluția generală a sistemului.
Din soluția generală găsim un sistem fundamental de soluții:
.
Cu ajutorul unui sistem fundamental de soluții, soluția generală poate fi scrisă în formă
.
Rezolvăm sistemul omogen de ecuații.
Matricea coeficienților are gradul 4, deoarece
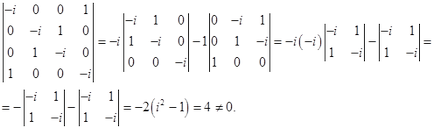
Deoarece rangul este egal cu numărul de necunoscute, sistemul are doar o soluție trivială.
Rezolvăm sistemul omogen de ecuații.
Matricea coeficienților are gradul 4, deoarece
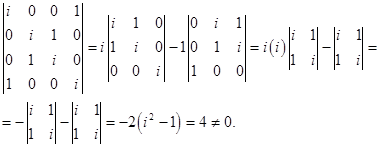
Deoarece rangul este egal cu numărul de necunoscute, sistemul are doar o soluție trivială.
Astfel, avem vectorii proprii u.
Alegem ca bază ortogonală vectorul ,,,.
Normalizăm baza ortogonală găsită: