Lucrarea poate fi folosită pentru a desfășura lecții și rapoarte în domeniul "Geometriei"
Această secțiune a site-ului a colectat toate prezentările educaționale despre geometrie. Prezentările pregătite în geometrie vor ajuta cadrele didactice să petreacă mai puțin timp pentru a desena forme geometrice complexe și mai mult pentru a lucra cu clasa pentru a rezolva problemele în sine. Prezentările privind geometria vor fi utile pentru profesorii și părinții care își ajută copiii cu o explicație a temelor lor. Puteți descărca prezentări gata pentru lecții de geometrie pentru gradele 6,7,8,9,10,11.

Informația este încorporată în imaginea de diapozitive.

Ce înseamnă geometria termenului? Ce înseamnă geometria termenului? Din istoria originii geometriei. Unde studiază geometria? Tipuri de unghiuri. Tipuri de triunghiuri. De ce aveți nevoie de geometrie. Și dacă nu ar exista geometrie. Surse de informații.
GEOMETRIE, o ramură a matematicii care studiază proprietățile diferitelor figuri (puncte, linii, unghiuri, obiecte bidimensionale și tridimensionale), dimensiunile și aranjamentul reciproc. Pentru comoditatea predării, geometria este împărțită în planimetrie și stereometrie. GEOMETRIE, o ramură a matematicii care studiază proprietățile diferitelor figuri (puncte, linii, unghiuri, obiecte bidimensionale și tridimensionale), dimensiunile și aranjamentul reciproc. Pentru comoditatea predării, geometria este împărțită în planimetrie și stereometrie.

Unul dintre cei mai renumiți ucenici ai lui Thales era Pitagora (aproximativ 570 - aproximativ 500 î.Hr.). A călătorit foarte mult și apoi sa stabilit în Crotone, Italia, unde a fondat o societate care a studiat aritmetica, muzica, geometria și astronomia. Pitagora și urmașii săi au demonstrat multe teorii noi despre triunghiuri, cercuri, proporții și unele corpuri tridimensionale. Pitagora a demonstrat, de asemenea, celebra teorema care îi poartă numele de astăzi, potrivit căreia suprafața de pătrat construit pe ipotenuzei unui triunghi dreptunghic este egală cu suma ariilor pătratelor construite pe Catete. Evul mediu. După căderea Alexandriei, majoritatea lucrărilor matematicienilor greci antic au fost împrăștiați sau pierduți. Unele dintre ele, inclusiv Elementul Euclid, au fost traduse și studiate de arabi și indieni. Cu toate că acești oameni au generat mai multe mari matematicieni, printre care cele mai cunoscute matematicieni indiene Aryabhata (cca 476 - .. Ca. 550) și Bhaskara II a (. Ca 1114-1185), dar cea mai mare meritul lor ar trebui să fie luate în considerare păstrarea geometriei în Evul Mediu.

Geometria este utilizată peste tot. Geometria cuvântului este în toate limbile lumii. Aceasta este o dovadă suplimentară a nevoii sale. în geometria engleză în germană Geometrie în franceză géométrie în geometria italiană în spaniolă geometría

În epoca noastră, geometria este o știință reală, studiată în toate școlile, universitățile și universitățile. În epoca noastră, geometria este o știință reală, studiată în toate școlile, universitățile și universitățile. În școli, copiii studiază acest subiect din clasa a VII-a. Geometria necesită o atenție specială și o pregătire atentă pentru lecție. Geometria este un lucru important în viața fiecărei persoane, deci este important să o tratezi cu mare importanță de la prima cunoștință.

Și cum să ne imaginăm viața fără figuri geometrice. Și cum să ne imaginăm viața fără figuri geometrice. Acum vă voi arăta diversitatea lor. Fără ei nu am putut trăi! Nici nu-ți poți imagina asta.
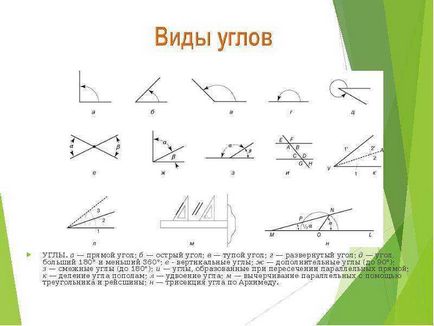
UNGHIURI. a este unghiul drept; b - unghi ascuțit; c - unghiul obtuz; r este unghiul dezvoltat; d este unghiul mai mare de 180 ° și mai mic de 360 °; e - unghiuri verticale; g - unghiuri suplimentare (până la 90 °); 3 - unghiuri adiacente (până la 180 °); u sunt unghiurile formate atunci când liniile paralele se intersectează; k este împărțirea unghiului în jumătate; l este dublarea unghiului; m - desen paralel cu ajutorul unui triunghi și a unui zbor; n este triajul unghiului de către Arhimede. UNGHIURI. a este unghiul drept; b - unghi ascuțit; c - unghiul obtuz; r este unghiul dezvoltat; d este unghiul mai mare de 180 ° și mai mic de 360 °; e - unghiuri verticale; g - unghiuri suplimentare (până la 90 °); 3 - unghiuri adiacente (până la 180 °); u sunt unghiurile formate atunci când liniile paralele se intersectează; k este împărțirea unghiului în jumătate; l este dublarea unghiului; m - desen paralel cu ajutorul unui triunghi și a unui zbor; n este triajul unghiului de către Arhimede.

Triangle. a - versatil; b este isoscele; c - echilateral; r - dreptunghiular; q - lungimile laturilor și segmentelor într-un triunghi dreptunghiular; e sunt unghiurile triunghiului; g - mediani; s - înălțimi; și bisectoare de unghiuri; k este un triunghi împărțit printr-o linie dreaptă paralelă cu una dintre laturi; l este un triunghi tăiat de un bisector al unuia dintre unghiuri; m - triunghiuri asemănătoare; n este un divizor proporțional. Triangle. a - versatil; b este isoscele; c - echilateral; r - dreptunghiular; q - lungimile laturilor și segmentelor într-un triunghi dreptunghiular; e sunt unghiurile triunghiului; g - mediani; s - înălțimi; și bisectoare de unghiuri; k este un triunghi împărțit printr-o linie dreaptă paralelă cu una dintre laturi; l este un triunghi tăiat de un bisector al unuia dintre unghiuri; m - triunghiuri asemănătoare; n este un divizor proporțional.

Regulile sunt amintite mai bine atunci când au o formulă hilară. Toată lumea știe că regulile sunt amintite mai bine atunci când au o formulă hilară. Toată lumea știe că "Bisectrix - Este un șobolan care se urcă în colțuri și împarte unghiul în jumătate." CCl - bisector al unghiului abc1

Pentru a stoca ca o rimă de benzi desenate a folosit teorema lui Pitagora: Pentru a stoca aceeași rima de benzi desenate a folosit teorema lui Pitagora: „! Pantaloni pitagoreice în toate direcțiile sunt egale“

Întrebare: Care dintre matematicieni vechi, a fost ucis de un soldat roman, cu mândrie exclamând: „Pleacă, nu atingeți desenele mele!“ Întrebare: Care dintre matematicieni vechi uciși de mâinile unui soldat roman, cu mândrie exclamând: „! Pleacă, nu atingeți desenele mele“ Reacționează: Cercetătorul grec este Archimedes. Găsiți scrisorile care lipsesc: 1. GMTR ZDCH 2. 3. 4. TRPTS PRPNDKLR Răspunsuri: 1. Geometrie 2. Problema 3. Linia 4. Perpendicular.

Trei în pătrat este 9. Patru în pătrat este 16. Și care este unghiul din pătrat? (90º) Trei pătrat este 9. Patru pătrate sunt 16. Și care este unghiul în pătrat? (90º) Care este numele unui triunghi ale cărui două părți sunt egale? (isoscele) Pot exista două unghiuri obtuze în triunghi? (nu) Care este numele aparatului pentru măsurarea unghiurilor? (protractor) Care este suma unghiurilor triunghiului? (180º) Care sunt numele liniilor care nu se intersectează într-un avion? (paralel) Care este numele unei paralelograme cu toate laturile egale și unghiurile drepte? (pătrat) Care este numele aparatului pentru măsurarea segmentelor? (conducător) Care este suma unghiurilor adiacente? (180º) Care sunt liniile care se intersectează într-un unghi drept? (Perpendicular)

Mulți studenți neglijenți în temele de studiu sunt puse o întrebare. "De ce este nevoie de geometrie?" Și, în general, nu va fi util pentru mine. De ce lecții! Haide! "Și mergeți la o plimbare! Dar nici măcar nu se gândesc cum să le folosească în viață! Atunci cum vor suferi în viitor! Mulți studenți neglijenți în temele de studiu sunt puse o întrebare. "De ce este nevoie de geometrie?" Și, în general, nu va fi util pentru mine. De ce lecții! Haide! "Și mergeți la o plimbare! Dar nici măcar nu se gândesc cum să le folosească în viață! Atunci cum vor suferi în viitor! De exemplu: va exista un astfel de student ca constructor, deoarece el va crea un plan de construcție dacă nu înțelege figurile geometrice sau nu știe cum să-i scaldeze. Și dacă, de exemplu, același elev a explicat copilului său acest subiect, ce ar spune el? Ar arăta rău în ochii copilului și să-i dea un exemplu rău! Din aceasta se poate concluziona că fără geometrie este foarte greu să trăiești!

Să încercăm să ne imaginăm că nu există o astfel de știință ca geometria, ceea ce înseamnă că o persoană nu știe cum se numește cifrele! Să încercăm să ne imaginăm că nu există o astfel de știință ca geometria, ceea ce înseamnă că o persoană nu știe cum se numește cifrele! Și cum să trăim așa. De exemplu, dacă veniți la magazin, uitați numele produsului, cum explicați ce produs doriți să cumpărați. Cel mai probabil vânzătorul nu va înțelege o astfel de explicație ca galben și gustos! Și cum va fi posibil să studiezi la școală, cum va fi posibil să explici la o consiliu ce formă formează pământul, o minge.

În toate diapozitivele, ți-am arătat dovada că geometria este necesară! Să o folosim cu detalii mici și toate acestea nu vă pot dovedi că este necesară geometria. Dar există o astfel de întrebare care face ca orice sceptic să creadă că este necesară! De ce au studiat oamenii vechi, învățații greci, învățații medievali? Proprietăți și teoreme au fost dovedite. De ce îl studiem acum, dacă nu avem nevoie de ea. Răspunsul este simplu și elementar - este necesar, pentru că fără el nu am avea nimic. În toate diapozitivele, ți-am arătat dovada că geometria este necesară! Să o folosim cu detalii mici și toate acestea nu vă pot dovedi că este necesară geometria. Dar există o astfel de întrebare care face ca orice sceptic să creadă că este necesară! De ce au studiat oamenii vechi, învățații greci, învățații medievali? Proprietăți și teoreme au fost dovedite. De ce îl studiem acum, dacă nu avem nevoie de ea. Răspunsul este simplu și elementar - este necesar, pentru că fără el nu am avea nimic.

Marea Enciclopedie Sovietică. Marea Enciclopedie Sovietică. Arhivele proprii. Enciclopedia "Krugosvet"