Definiția. O relație binară R este o submulțime de perechi (a, b) ∈ R a produsului cartesian A × B, adică, R⊆A × B. În acest caz, mulțimea A este numită domeniu de definire a relației R, setul B este intervalul de valori.
Denumire: aRb (adică a și b sunt în raport cu R). /
Notă. dacă A = B. atunci spunem că R este o relație pe setul A.
Metode pentru specificarea relațiilor binare
1. O listă (enumerarea de perechi) pentru care această relație este îndeplinită.
2. Matricea. O relație binară R ∈ A × A. unde A = (a1, a2.An) corespunde unei matrice pătrate de ordine n. în care elementul cij. care este la intersecția rândului i și a coloanei j, este 1 dacă există o relație R între ai și aj sau 0 dacă este absent:
Fie R o relație pe setul A, R ∈ A × A. Apoi raportul R:
este reflexivă dacă Ɐ a ∈ A: a R a (principala diagonală a matricei relației reflexive conține numai una);
este antireflexiv dacă Ɐ a ∈ A: a R a (diagonala principală a matricei reflexive conține numai zerouri);
simetric dacă Ɐ a. b ∈ A: a R b ⇒ b R a (matricea acestui raport este simetrică față de diagonala principală, adică, cij cji);
este antisimetric dacă Ɐ a, b ∈ A: a R b b R a ⇒ a = b (nu există unități în matricea unui astfel de raport care să fie simetric în raport cu diagonala principală);
este tranzitorie dacă Ɐ a, b, c ∈ A: a R b b R c ⇒ o Rc (în această relație matrice trebuie satisfăcută: .. dacă rândul i-lea este o unitate, de exemplu în coordonate liniile j-lea (coloana), adică cij = 1. atunci toate unitățile din j- (aceste unități să corespundă cu k e coordonate astfel încât, cjk = 1) trebuie să corespundă celor din rândul i din aceleași coordonate k, adică cik = 1 (și, poate, și în alte coordonate).
Problema 3.1. Definiți proprietățile relației R - "a fi un divizor", dat pe setul de numere naturale.
reflexiv, nu antireflexiv, deoarece orice număr se împarte fără un rest: a / a = 1 pentru toate a∈N;
nu simetric, antisimetric, de exemplu, 2 divizor 4, dar 4 nu este un divizor 2;
transitiv, deoarece b / a ∈ N și c / b ∈ N, c / a = b / a ⋅ c / b ∈ N, de exemplu, dacă 6/3 = 2∈N și 18/6 = 3∈N, 18/3 = 18 / 6⋅6 / 3 = 6∈N.
Problema 3.2. Definiți proprietățile relației R - "fii un frate", dat pe un set de persoane.
Soluția.
nu reflexiv, antireflexiv din cauza absenței evidente a aRa pentru toate a;
nu este simetrică, deoarece în cazul general aRb are loc între fratele a și sora b. dar nu bRa;
nu este antisimetric, deoarece dacă a și b sunt frați, atunci aRb și bRa, dar a ≠ b;
tranzitiv, dacă numesc frați ai unor persoane care au părinți obișnuiți (tată și mamă).
Sarcina 3.3. Definiti proprietatile relatiei R - "a fi seful", dat pe setul de elemente ale structurii
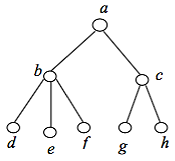
- Nu este reflexiv, antireflexiv, dacă într-o interpretare concretă nu are sens;
- nu este simetrică, antisimetrică, deoarece pentru toți a ≠ b aRb și bRa nu sunt îndeplinite simultan;
- tranzit, deoarece dacă a este șeful B și b este șeful c. apoi un sef c.
Sarcini pentru soluții independente
Determinați proprietățile relației Ri. dată pe setul Mi printr-o matrice, dacă:
Operații privind relațiile binare
Să presupunem că R1. R1 este o relație definită pe setul A.
Definirea gradului de relație R pe setul A este compoziția sa cu ea însăși.
Definiția. Dacă R ⊂ A × B. atunci R º R -1 este numit kernelul relației R.
TEOREM 3.1. Fie R ⊂ A × A relatia definita pe setul A.
- R este reflexiv dacă și numai dacă (⇔) este folosit mai târziu atunci când I ⊂ R.
- R este simetric ⇔ R = R -1.
- R este tranzitiv ⇔ R º R ⊂ R
- R este antisimetrică ⇔ R ⌒ R -1 ⊂ I.
- R este antireflexivă ⇔ R ⌒ I = ∅.
Problema 3.4. Fie R relația dintre seturi și dată de enumerarea perechilor: R =. În plus, S este relația dintre seturile S =. Calculați R-1. S -1 și S º R. Verificați că (S º R) -1 = R -1. S -1.
Sarcina 3.5. Fie R raportul n. părinte. ", Iar S este raportul". frate. "Pe setul tuturor oamenilor. Faceți o scurtă descriere verbală a relației:
R-1. S -1. R º S, S -1 º R -1 și R º R.
R -1 este raportul ". copil. „;
S -1 este raportul dintre ". frate sau sora. „;
R º S este raportul ". părinte. „;
S -1 º R -1 este raportul dintre. copil. "
R º R este raportul dintre ". bunica sau bunicul. "
Sarcini pentru soluții independente
1) Fie R raportul n. tată. ", Iar S este raportul". sora. "Pe setul tuturor oamenilor. Oferiți o descriere verbală a relației:
R-1. S -1. R º S, S -1 º R -1. R º R.
2) Fie R raportul n. frate. ", Iar S este raportul". mama. "Pe setul tuturor oamenilor. Oferiți o descriere verbală a relației:
R-1. S -1. S º R, R -1 º S -1. S º S.
3) Fie R raportul n. bunicul. ", Iar S este raportul". fiule. "Pe setul tuturor oamenilor. Oferiți o descriere verbală a relației:
R-1. S -1. R º S, S -1 º R -1. S º S.
4) Fie R raportul n. fiică. ", Iar S este raportul". bunica. "Pe setul tuturor oamenilor. Oferiți o descriere verbală a relației:
R-1. S -1. S º R, R -1 º S -1. R º R.
5) Fie R raportul n. nepoata. ", Iar S este raportul". tată. "Pe setul tuturor oamenilor. Oferiți o descriere verbală a relației:
R-1. S -1. S º R, R -1 º S -1. R º R.
6) Fie R relația "sora". ", Și S este relația" mama. "Pe setul tuturor oamenilor. Oferiți o descriere verbală a relației:
R-1. S -1. R º S, S -1 º R -1. S º S.
7) Fie R raportul n. mama. ", Iar S este raportul". sora. "Pe setul tuturor oamenilor. Oferiți o descriere verbală a relației:
R-1. S1, R º S, S1 º R1, S º S.
8) Fie R raportul n. fiule. ", Iar S este raportul". bunicul. "Pe setul tuturor oamenilor. Oferiți o descriere verbală a relației:
R-1. S -1. S º R, R -1 º S -1. R º R.
9) Fie R raportul n. sora. ", Iar S este raportul". tată. "Pe setul tuturor oamenilor. Oferiți o descriere verbală a relației:
R-1. S -1. R º S, S -1 º R -1. S º S.
10) Fie R raportul n. mama. ", Iar S este raportul". frate. "Pe setul tuturor oamenilor. Oferiți o descriere verbală a relației:
R-1. S -1. S º R, R -1 º S -1. R º R.