Vom începe prin a discuta energia potențială pe care o are încărcarea într-un câmp electrostatic. În primul rând, este necesar să ne amintim în ce condiții conceptul de energie potențială poate fi introdus deloc.
3.4.1 Forțele conservatoare
Forța este numită conservatoare (sau potențial) dacă lucrarea acestei forțe nu depinde de forma traiectoriei și este determinată numai de poziția inițială și finală a corpului.
Să, de exemplu, un organism sub acțiunea unei forțe conservatoare
mutat de la inițial
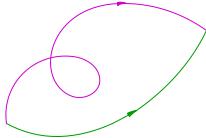
punctul 1 până la punctul final 2 (Figura 3.16). Apoi munca de forță
depinde doar de situație
ele însele punctele 1 și 2, dar nu din traiectoria mișcării corpului. De exemplu, pentru traiectorii 1. a. 2 și 1. b. 2 valoarea lui A va fi aceeași.
Fig. 3.16. Pentru noțiunea de forță conservatoare
Rețineți că munca unei forțe conservatoare de-a lungul oricărei căi închise este zero. Într-adevăr, să ieșim din punctul 1 de-a lungul traiectoriei 1. a. 2 și întoarceți-vă de-a lungul căii 2. b. 1. Pe prima traiectorie forța va funcționa A, iar pe a doua traiectorie munca va fi egală cu A. Ca rezultat, munca totală va fi zero.
Deci, conceptul de energie potențială poate fi introdus doar în cazul unei forțe conservatoare. Energia potențială W este o expresie matematică care depinde de coordonatele corpului, astfel încât lucrarea forței este egală cu schimbarea acestei expresii cu un semn minus:
Sau, care este același:
A = (W 2 W 1) = W 1 W 2:
După cum vedem, munca unei forțe conservatoare este diferența dintre valorile energiei potențiale, calculate pentru pozițiile inițiale și finale ale corpului.
Exemple de forțe conservatoare vă sunt bine cunoscute. De exemplu, gravitatea este conservatoare. Elasticitatea arcului este de asemenea conservatoare. De aceea, putem vorbi despre energia potențială a unui corp ridicat deasupra solului sau despre energia potențială a unui izvor deformat.
Dar forța de frecare nu este conservatoare: forța forței de frecare depinde de forma traiectoriei și nu este egală cu zero pe calea închisă. Prin urmare, nu există nici o potențială energie a corpului în câmpul de forță al frecării.
3.4.2 Potențialitatea câmpului electrostatic
Se pare că forța cu care câmpul electrostatic acționează asupra unui corp încărcat este, de asemenea, conservatoare. Lucrarea acestei forțe, efectuată atunci când încărcarea este mișcată, se numește lucrarea câmpului electrostatic. Prin urmare, avem cel mai important fapt:
Lucrarea câmpului electrostatic nu depinde de forma traiectoriei de-a lungul căreia se deplasează sarcina și este determinată numai de pozițiile inițiale și finale ale încărcăturii. Munca câmpului de-a lungul căii închise este zero.
Acest fapt se mai numește și potențialul câmpului electrostatic. Ca și domeniul gravitațional, câmpul electrostatic este potențial. Lucrarea câmpului electrostatic este aceeași pentru toate căile prin care încărcarea se poate deplasa de la un punct fix al spațiului la altul.
O dovadă matematică riguroasă a potențialului câmpului electrostatic depășește domeniul de aplicare al curriculumului școlar. Cu toate acestea, la nivelul fizic al rigidității, putem verifica validitatea acestui fapt utilizând următorul argument simplu.
Este ușor de observat că dacă câmpul electrostatic nu ar fi potențial, atunci ar fi posibil să construim o mașină de mișcare perpetuă! De fapt, atunci ar fi o traiectorie închisă, atunci când se va deplasa o sarcină de-a lungul căreia câmpul ar face o treabă pozitivă (și nu s-ar produce schimbări în corpurile înconjurătoare). Twist o taxă pe această cale, vom trage o cantitate nelimitată de energie de nicăieri și toate problemele sunt rezolvate de energie :-) Dar, din păcate, nu ma uit la ea contrazice flagrant legea conservării energiei.
Din moment ce câmpul electrostatic este potențial, putem vorbi despre energia de încărcare potențială în acest domeniu. Să începem cu un caz simplu și important.
3.4.3 Energia potențială a unei încărcări într-un domeniu omogen
Energia potențială a unui corp ridicat deasupra solului este mgh. Cazul unei încărcări într-un domeniu omogen se dovedește a fi foarte asemănător cu această situație mecanică.
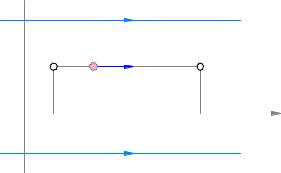
Luați în considerare un câmp electrostatic omogen E, ale cărui linii sunt orientate de-a lungul axei X (Figura 3.17). Permiteți încărcarea pozitivă q să se deplaseze de-a lungul liniei electrice de la punctul 1 (cu coordonatele x 1) până la punctul 2 (cu coordonate x 2).
Fig. 3.18. Transfer de taxe într-un domeniu omogen
Trecerea de la punctul 1 la punctul 2, să aleagă calea 3. 1. 2, în cazul în care punctul 3 se află pe aceeași linie de alimentare cu punctul 1. Apoi, lucrările 32 pe o secțiune 32 este zero, pentru că ne mișcăm forță perpendiculară. Ca rezultat, obținem:
A = A 13 + A 32 = A 13 = qE (x 2 x 1):
Vedem că lucrarea câmpului depinde numai de abscisele pozițiilor inițiale și finale ale acuzației. Se scrie formula care rezultă după cum urmează:
A = qEx 2 qEx 1 = ((qEx 2) (qEx 1)) = (W 2 W 1) = W:
Aici W 1 = qEx 1. W 2 = qEx 2. Munca câmpului, în conformitate cu formula (3.8), este egală cu schimbarea cu semnul minus al cantității
Această cantitate reprezintă energia de încărcare potențială într-un câmp electrostatic omogen. X reprezintă abscisa punctului în care se caută energia potențială. Nivelul zero al energiei potențiale corespunde, în acest caz, originii coordonatelor x = 0 iar în cifre este reprezentat de o linie punctată perpendiculară pe liniile de tensiune 4.
Amintiți-vă că pentru moment q> 0. Din formula (3.9) rezultă că atunci când sarcina se deplasează de-a lungul liniei de forță, energia potențială scade cu creșterea x. Acest lucru este normal: câmpul face o treabă pozitivă, accelerarea încărcării, iar energia cinetică a încărcăturii crește datorită pierderii energiei sale potențiale.
Este ușor de arătat că formula (3.9) rămâne valabilă pentru q <0. В этом случае потенциальная энергия возрастает с ростом x. Это тоже понятно: ведь сила, с которой поле действует на заряд, теперь будет направлена влево, так что движение заряда вправо будет осуществляться против действия поля. Заряд тормозится полем, кинетическая энергия заряда уменьшается, а потенциальная энергия увеличивается.
Deci, o concluzie importantă: în formula pentru energia potențială, q denotă magnitudinea algebrică a sarcinii (cu semnul în minte) și nu modulul său.
4 De fapt, nivelul zero al energiei potențiale poate fi ales oriunde. Cu alte cuvinte, energia potențială este determinată numai până la o constantă aditivă arbitrară C, adică W = qEx + C. Nu este nimic de îngrijorat în această incertitudine: energia fizică are înțelesul fizic în sine și diferența de potențiale energii, egală cu munca pe teren. În această diferență, constanta C scade.
3.4.4 Energia potențială de interacțiune a tarifelor punctuale
Permiteți încărcării cu două puncte q 1 și q 2 să fie în vid la o distanță r una de cealaltă. Se poate arăta că energia potențială a interacțiunii lor este dată de formula:
Luăm formula (3.10) fără dovadă. Două caracteristici ale acestei formule ar trebui discutate.
În primul rând, unde este nivelul zero al energiei potențiale? Până la urmă, energia potențială, așa cum se poate observa din formula (3.10), nu poate dispărea. Dar, în realitate, nivelul zero există și este la infinit. Cu alte cuvinte, când încărcăturile se află infinit departe una de cealaltă, se presupune că energia potențială a interacțiunii lor este zero (ceea ce este logic în acest caz, încărcările nu interacționează deja).
În al doilea rând, q 1 și q 2 sunt din nou cantități algebrice de taxe, adică taxele luând în considerare semnul lor.
De exemplu, energia potențială a interacțiunii a două încărcări cu același nume va fi pozitivă. De ce? Dacă îi eliberăm, vor începe să se accelereze și să se îndepărteze unul de celălalt. Energia lor cinetică crește, astfel că energia potențială scade. Dar, la infinit, energia potențială dispare și din moment ce scade la zero, înseamnă că este pozitivă.
Dar energia potențială a interacțiunii diferitelor sarcini este negativă. Într-adevăr, să le eliminăm o distanță foarte mare una de cealaltă, astfel încât energia potențială să fie zero și să renunțe. Taxele vor începe să se accelereze, se apropie, iar energia potențială scade din nou. Dar dacă era zero, atunci unde merge? Numai în direcția valorilor negative.
Formula (3.10) ajută, de asemenea, la calcularea energiei potențiale a unui sistem de taxe, în cazul în care numărul de taxe este mai mare de două. Pentru a face acest lucru, trebuie să însumați energiile fiecărei perechi de taxe. Nu vom scrie formula generală; să ilustreze mai bine ceea ce sa spus printr-un exemplu simplu, prezentat în Fig. 3,19.
Fig. 3,19. Interacțiunea a trei sarcini
Dacă sarcinile q 1. q 2. q 3 se află la vârfurile triunghiului cu laturile a, b, c, atunci energia potențială a interacțiunii lor este egală cu: