1. Evaluează momentul forței de frânare care acționează asupra corpului în timpul rotirii.
2. Determinați momentul de inerție a corpului luând în considerare momentul forței de frânare.
3. Calculați momentele folosind relațiile de energie.
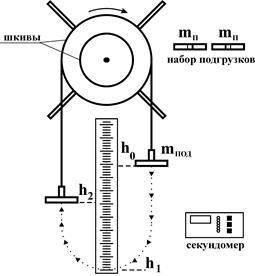
Instalarea este un corp cu scripete care se rotește în rulmenți cu bile. Un fir este înfășurat pe scripete, un capăt al căruia este atașat de scripete, iar celălalt pe suport cu o masă. Suportul poate fi încărcat cu o masă pe suport. Sarcina poate fi coborâtă prin gravitate, determinând rotirea corpului. După ce sarcina de la marcajul h0 scade până la lungimea totală a firului până la marca h1 (vezi figura 4.1), corpul, care se rotește prin inerție, va ridica din nou încărcătura la o anumită înălțime până la marca h2.
În procesul de mișcare, o parte din energia mecanică a sistemului de încărcare corporală este folosită pentru a lucra împotriva forței de frânare și, prin urmare, se transformă în energia internă a sistemului și a aerului înconjurător, care sunt încălzite. Rezultă că corpul va ridica sarcina la o înălțime mai mică decât cea inițială, adică semnul h2 va fi întotdeauna sub marcajul h0. Forța de frânare constă în forța de frecare din lagăre și forța de frecare a aerului pe măsură ce corpul și încărcătura se mișcă.
CONCLUZII FORMULARE DE LUCRU
Derivarea formulei pentru măsurarea indirectă a momentului forței de frânare
Pentru a estima momentul forței de frânare, folosim relațiile energetice. Deoarece forțele de fricțiune sunt disipative, activitatea forței de frânare AT în timpul trecerii sistemului de greutate corporală de la starea inițială la starea finală este egală cu
unde este energia mecanică a sistemului de încărcare corporală în stare inițială;
- energia mecanică a sistemului de încărcare corporală în stare finală.
Energia mecanică a sistemului constă în energii cinetice și potențiale. În momentele în care sistemul este în repaus, energia cinetică este zero și, prin urmare, energia mecanică devine egală doar cu energia potențială a sistemului. Astfel de stări ale sistemului apar în momentul inițial al momentului, când încărcătura se află la marcă. și în momentul în care, după coborârea în jos, sarcina crește până la marcaj datorită rotației corpului (figura 4.1). Dacă presupunem că energia de sarcină potențială la altitudine este zero, creșterea energiei mecanice pentru stările inițiale și finale selectate ale sistemului este
unde este distanța dintre mărci și;
- distanța dintre semne și.
Vom presupune că momentul forței de frânare este în principal asociat cu mișcarea de rotație a corpului, adică forța de frânare care acționează asupra sarcinii este neglijată. Apoi lucrarea elementară a momentului forței de frânare este egală cu produsul scalar
,
unde este vectorul de moment al forței de frânare;
- vector al deplasării unghiulare infinitezimale a unui corp.
Ambii vectori sunt direcționați de-a lungul axei de rotație, dar în direcții opuse. Prin urmare,
.
Lucrarea completă a cuplului forței de frânare, dacă se presupune că este constantă, este atunci
unde este unghiul de rotație a corpului în jurul axei în timpul trecerii sistemului de la starea inițială la starea finală (sarcina se deplasează apoi de la marcă la marcaj).
Când deplasați sarcina în jos de la marcaj spre marcaj de pe scripete, un fir este înfășurat în lungime. Având în vedere că circumferința roții este egală și fiecare rotire a roții corespunde unghiului radianilor, găsim unghiul de rotație al scripetei când sarcina se deplasează în jos:
Evident, cu rotația suplimentară a corpului până în momentul în care încărcarea se oprește la marcaj. se va transforma într-un unghi
Apoi, unghiul de rotație total al corpului, corespunzător tranziției încărcăturii de la marcă la marcă. este
Substituind (4.2) și (4.3) în (4.1), găsim
.
Din aceasta, folosind (4.5), obținem o formulă pentru estimarea modulului vectorului de moment al forței de întârziere