Sarcina 14. Se dă o prismă hexagonală obișnuită, lungimile tuturor marginilor cărora sunt egale cu 1.
a) Construiți o secțiune care trece prin două muchii opuse ale bazelor prismei.
b) Găsiți zona secțiunii.
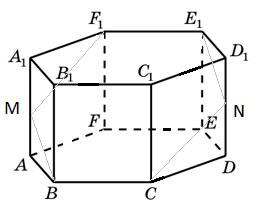
a) Două margini opuse ale prismei hexagonale obișnuite, de exemplu marginile BC și. Secțiunea trasată prin aceste margini va fi un hexagon care trece prin punctele M și N, situate în mijlocul segmentelor și respectiv (vezi figura).
b) Să presupunem că unghiul dintre secțiune și baza prismei este. Apoi putem scrie următoarea egalitate
unde este aria bazei prismei; este aria secțiunii necesare. Din această formulă exprimăm aria transversală, obținem:
Gasim din triunghiul drept BFF1 raportul dintre piciorul adiacent BF si hypotenuse BF1. Să găsim partea BF din triunghiul ABF. La acest triunghi, unghiul A este de 120 de grade. Laturile AB și AF sunt egale cu 1. Apoi, prin teorema cosinusului avem:
Acum, luați în considerare un triunghi dreptunghiular și calculați partea de teorema lui Pitagora:
Astfel, cosinusul unghiului dintre planuri este egal cu
Acum calculați aria bazei prismei. Deoarece baza este un hexagon obișnuit, ea poate fi divizată în 6 triunghiuri echilaterale ale căror laturi sunt egale cu 1 (deoarece toate fețele bazei sunt egale cu 1). După cum se știe, aria unui triunghi echilateral este egală cu și pentru a = 1 avem. Apoi, zona hexagonului este
În cele din urmă, zona secțiunii transversale va fi