În geometria descriptivă, foarte des se rezolvă problemele pentru a determina cantitățile metrice de obiecte prin proiecțiile lor. Una dintre cele mai frecvente probleme este problema determinării valorii naturale a unei poziții generale directe din proiecțiile sale. Există mai multe modalități de a rezolva această problemă, dintre care una este o metodă de triunghi dreptunghic utilizat într-o varietate de sarcini complexe, generalizate geometriei descriptive, de exemplu, atunci când se determină distanța dintre două puncte în spațiu, iar lungimea reală a marginilor poliedre laturi ale poligoanelor, și așa mai departe. D.
Reprezentăm în spațiu o linie de poziție generală dată de un segment AB. localizate în mod arbitrar. segmentul de înclinare unghiuri ale fiecărui plan de proiecție este diferită și, prin urmare, fiecare proiecții plane ale segmentului AB este afișat cu o distorsiune diferită. Din fig. 25, dar putem concluziona că segmentul AB este hypotenuse a triunghiului drept AB1. în care un cathet este egal cu proiecția segmentului A1. iar celălalt picior este egal cu diferența dintre distanțele până la capetele segmentului AB planul P1, adică egal otrezkuV1 = BB1 - .. AA1.
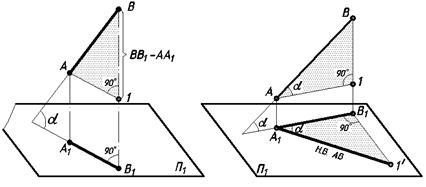
Unghiul unei linii drepte cu planul de proiecție este definit ca unghiul format de linia dreaptă cu proeminența sa pe planul dat. Același unghi intră în același triunghi dreptunghiular, care este construit pentru a determina valoarea naturală a unei linii drepte sau a unui segment de linie dreaptă. În Fig. 25, a și b sunt unghiul a.
Dacă sunt cunoscute picioarele triunghiului AB1. acesta poate fi construit oriunde în desen. Utilizați de obicei o anumită proiecție a segmentului. În Fig. 25b, pentru a găsi valoarea naturală a segmentului AB, este construit un triunghi dreptunghiular pe planul P1. Pentru aceasta, o perpendiculară pe proiecția A1 B1 este restaurată din punctul B1. reprezentate pe acest interval perpendicular AV diferența distanță se termină înainte de P1 plane (= BB1 BB1 - AA1). Segmentul A1 1 'de pe planul de proiecție va determina valoarea naturală a segmentului AB. În acest caz, unghiul a este unghiul de înclinare al segmentului AB față de planul proeminențelor П1.
Această metodă de determinare a cantității naturale a unei poziții generale drepte se numește metoda unui triunghi drept. și poate fi rezumată după cum urmează: dimensiunea reală a segmentului liniei este ipotenuza unui triunghi dreptunghic cu cateta din care este orice proiecție a acestui segment, iar celălalt - diferența dintre distanța dintre punctele finale la planul de proiecție.
Panta liniei drepte către planul orizontal al proeminențelor P1 este de obicei indicată prin simbolul a. la planul frontal al proeminențelor P2-b. planul de profil -g.
Schema luată în considerare este utilizată pentru a găsi valoarea naturală a liniei în poziție generală pe diagrama Monge pentru orice plan de proiecții. Această metodă este, de asemenea, utilizată pentru a rezolva problemele cu diferite variante de condiții date. De exemplu, în Fig. 26 oferă o soluție la problema în care se determină valoarea naturală a liniei drepte în planul profilului proeminențelor.
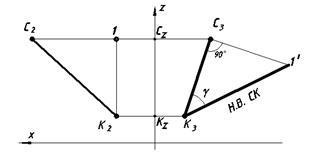
Pentru a face acest lucru, perpendicularul C3 1 'este reconstruit de la punctul C3 la proiecția de profil a liniei drepte C3 K3. Lungimea perpendiculară este egală cu diferența dintre segmentul CK și planul profilului proeminențelor, adică segmentului C2. care este egal cu diferența C2 Cz - K2 Kz. Pe planul profilului proiecțiilor conectați punctele K3 și 1 '. obținând astfel valoarea naturală a segmentului SK. Unghiul g între proiecția segmentului și valoarea sa naturală va determina unghiul de înclinare al segmentului CK față de planul profilului proiecțiilor.
În Fig. 27 este luată în considerare soluția problemei în care este necesară construirea unei proiecții orizontale a segmentului BC. dacă este dată proiecția frontală și unghiul b este unghiul de înclinare al segmentului BC față de planul frontal al proiecțiilor -P2.
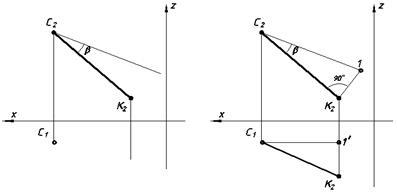
În Fig. 27a, iar starea problemei este prezentată în Fig. 27, soluție b. Pentru a rezolva problema, perpendicularul pe proiecția C2 R2 este restabilit de la punctul R2 și continuă până la punctul 1. Segmentul C2 1 va determina valoarea naturală a segmentului CK. în consecință, segmentul K2 1 este egal cu diferența dintre capetele segmentului CK față de planul frontal al proeminențelor. Pentru a construi o proiecție orizontală a segmentului SK din punctul C1, trageți o linie paralelă cu axa x. la extinderea liniei de comunicare de la punctul 1 'în jos, am setat distanța egală cu segmentul K2 1. și obține punctul K1. Conectând punctele C1 și K1. obținem o proiecție orizontală a segmentului CK. ceea ce a fost necesar pentru a rezolva problema.
Întrebări pentru auto-examinare
1. Care linie dreaptă se numește linie generală?
2. Care sunt liniile drepte ale liniilor poziției particulare?
3. Care sunt liniile drepte numite nivele?
4. Introduceți cuvântul lipsă: "Linia orizontală este linia, ... planul orizontal al proeminențelor" .5. Care proiecții drepte sunt întotdeauna verticale în același timp pe planurile orizontale și frontale ale proiecțiilor?