a) Numerele complexe sunt reprezentate de punctele planului conform următoarei reguli: a + bi = M (a; b) (figura 1).
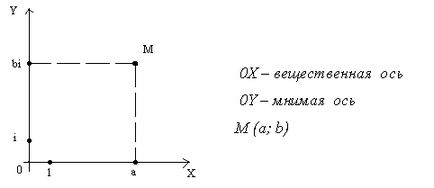
b) Numarul complex poate fi reprezentat de un vector care are un inceput la punctul O si un capat la un anumit punct (figura 2).
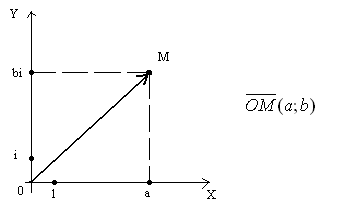
Exemplul 7. Puncte constructive reprezentând numere complexe: 1; - i; - 1 + i; 2 - 3i (figura 3).
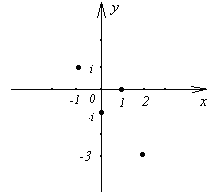
Notarea trigonometrică a numerelor complexe.
Numărul complex z = a + bi poate fi specificat folosind vectorul de rază cu coordonatele (a; b) (figura 4).
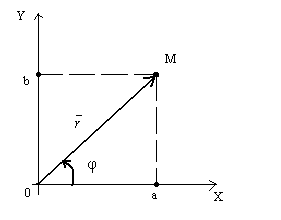
Definiția. Lungimea vectorului. care reprezintă numărul complex z. se numește modulul acestui număr și este notat cu r.
Pentru orice număr complex z, modulul său r = | z | este determinată în mod unic de formula.
Definiția. Valoarea unghiului dintre direcția pozitivă a axei reale și a vectorului. reprezentând un număr complex, se numește argumentul acestui număr complex și este notat de Arg z sau # 966; .
Argumentul numărului complex z = 0 nu este definit. Argumentul unui număr z complex ≠ 0 - valoarea multivaloare și este determinată într-un termen 2πk (k = 0 - 1, 1, - 2; 2; ...): Arg z = arg z + 2πk. unde arg z - valoarea principală a argumentului cuprins în intervalul (-π, π] adică -π. a = r · cos # 966; b = r · sin # 966; . Prin urmare, numărul complex z = a + bi poate fi scris în forma: z = r · cos # 966; + i r sin # 966; sau z = r + (cos # 966; + i păcat # 966;). O astfel de înregistrare a unui număr complex se numește forma trigonometrică a unui număr complex. Exemplul 8. Prezent în formă trigonometrică un număr complex 1 - i.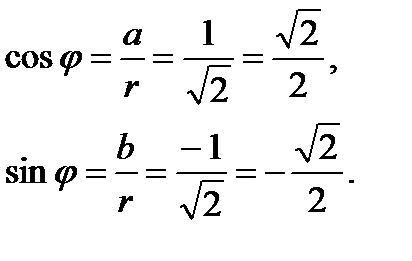
1 - i = (cos + i sin).