Există următoarele forme de numere complexe: algebrice (x + iy), trigonometrice (r (cos
Orice număr complex z = x + iy poate fi reprezentat pe planul XOY sub forma punctului A (x, y).
Planul pe care sunt reprezentate numerele complexe se numește planul variabilei complexe z (pe planul pe care îl punem simbolul z).
Axa OX este axa reală, adică pe ea există numere reale. OU este o axă imaginară cu numere imaginare.
x + iy este forma algebrică a numărului complex.
Luăm forma trigonometrică a notării unui număr complex.
;
Substituim valorile obținute în forma inițială, adică
r (cos
Forma exponențială a notării unui număr complex este dată de formula lui Euler :, atunci
z = rei
Acțiuni pe numere complexe.
3. multiplicare. z1 z2 = (x1 + iy1) * (x2 + iy2) = x1x2 + i (x1y2 + x2y1 + iy1y2) = (x1x2-y1y2) + i (x1y2 + x2y1);
4. diviziune. z1 / z2 = (x1 + iy1) / (x2 + iy2) = [(x1 + iy1) * (x2-iy2)] / [(x2 + iy2) * (x2-iy2)] =
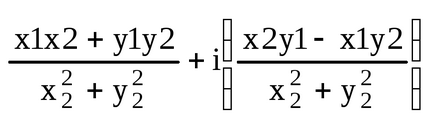
Două numere complexe care diferă numai în semnul unității imaginare, adică z = x + iy (z = x-iy), se numesc conjugate.
- Dacă sunt date numere complexe în formă trigonometrică.
Apoi produsul z1 * z2 al numerelor complexe este :; modulul produsului este egal cu produsul modulelor, iar argumentul produsului este egal cu suma argumentelor factorilor.
- Dacă numerele complexe sunt date în formă exponențială.
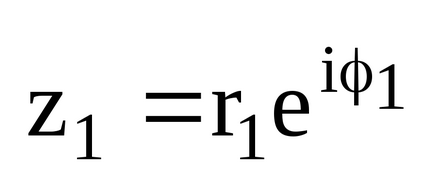
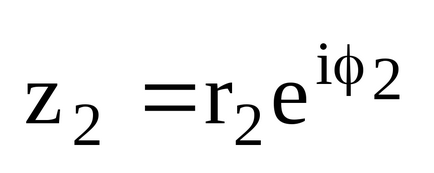
- Dacă sunt date numere complexe în formă trigonometrică.
- Dacă numerele complexe sunt date în formă exponențială.
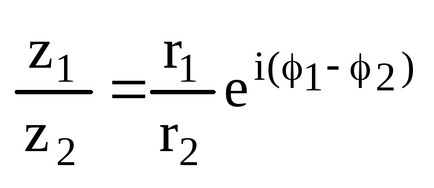
Exponentiation.
1. Numărul complex este dat în formă algebrică.
z = x + iy, atunci găsim z n prin formula binomică Newton:
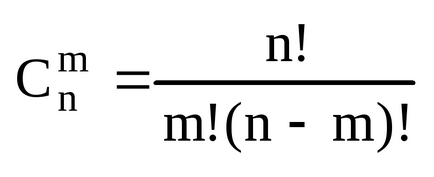
Îl aplicăm pentru un număr complex.
În expresia obținută, este necesar să se înlocuiască puterile lui i prin valorile lor:
i 0 = 1 Prin urmare, în cazul general obținem: i 4k = 1
i 31 = i 28 i3 = -i
i 1063 = i 1062 i = i
2. Dacă numărul complex este dat în formă trigonometrică.
Aici, n poate fi fie "+", fie "-" (întreg).
3. Dacă numărul complex este dat în formă exponențială:
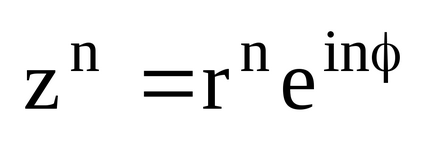
Soluția sa este a n-a rădăcină a numărului complex z:
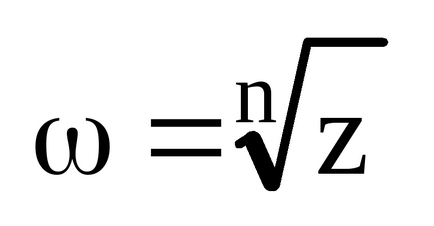
Radiația n a numărului complex z are exact n soluții (valori). Rădăcina puterii n-a efective are doar o singură soluție. În soluții complexe.
Dacă numărul complex este dat în formă trigonometrică:
z = r (cos
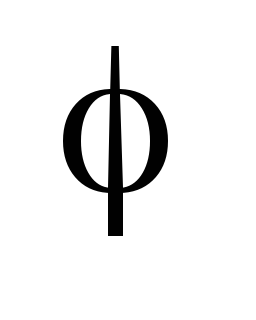
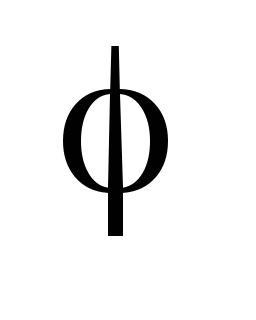
Ranks. Serii numerice.
Fie variabila a lua succesiv valorile a1, a2, a3, ..., an. Un astfel de set enumerat de numere se numește o secvență. Este infinit.
O serie numerică este expresia a1 + a2 + a3 + ... + an + ... =
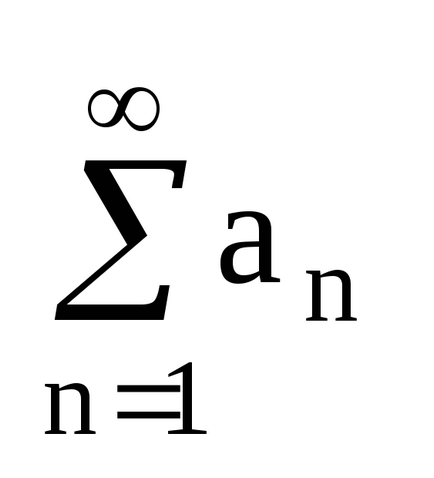
a1 este primul termen al seriei.
și n este al n-lea sau termen general al seriei.
O serie este considerată dată dacă este cunoscută a (a termenului comun al seriei).
Seria numerică are un număr infinit de termeni.
Numerele sunt o evoluție aritmetică (1,3,5,7 ...).
Numitorul este o progresie geometrică. bn = b1 qn-1;
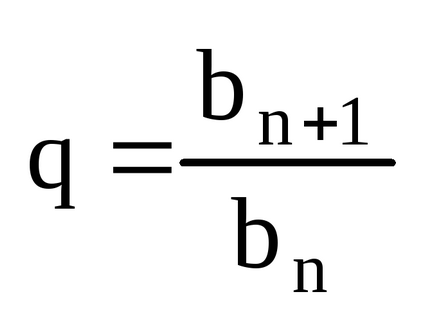
Luați în considerare suma primelor n termeni ai seriei și indicați-o de Sn.
Sn este a șaptea sumă parțială a seriei.
Seria converge. dacă această limită este finită (limita finită S există).
Seria este divergentă. dacă această limită este infinită.
În viitor, sarcina noastră este de a stabili care serii.
Una dintre cele mai simple, dar adesea întâlnite serii este o progresie geometrică.
Progresia geometrică este o secvență convergentă. dacă
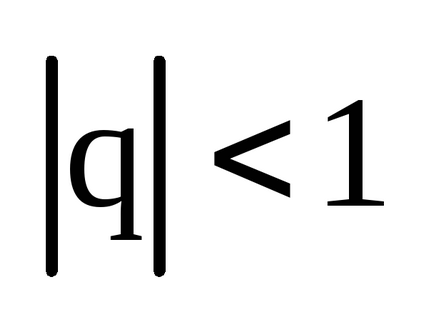
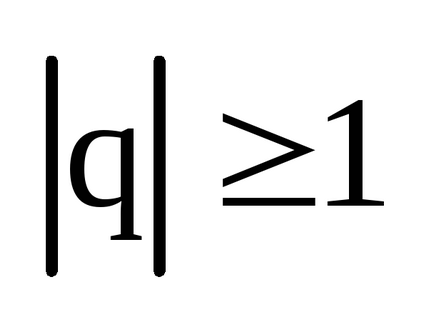
Există, de asemenea, o serie armonică (serie). Această serie este diferită.