Minimizarea funcțiilor. Hărți ale lui Carnot. Tehnologie digitală // EG Lab [14:20]
Forma normală disjunctivă minimă (MDNF) pentru o funcție logică este o disjuncție cu un număr minim de conjuncții elementare cu un număr minim de argumente (fie ele însele, fie negările lor) ale acestei funcții. În acest caz, tabelele de adevăr pentru funcția logică și MDNF sunt aceleași.
Forma normală disjunctivă minimă pentru o funcție logică cu numărul de argumente până la patru poate fi construită folosind hărți Carnot. Pentru aceasta, unitățile din harta Carnot sunt acoperite succesiv prin dreptunghiuri 4 × 2, 2 × 4, 2 × 2, 4 × 1, 1 × 4, 2 × 1, 1 × 2 și 1 × 1. Apoi sunt construite conjuncte elementare ale MDNF.
n este numărul de argumente pentru funcție;
k este numărul de dreptunghiuri pe harta lui Carnot;
argj (i, 1) este valoarea argumentului xj din argumentul setat pentru celula (i, l);
[Math] f_ (x_1, x_2, \ ldots, x_n) = \ bigcup \ limits_ ^ k \ bigcap \ limits_ \ arg_j \ stânga [P_t (x_1, x_2, \ ldots, x_n) = 1 \ right] = 1 \ text \\\ arg_j \ stânga [P_t (x_1, x_2, \ ldots, x_n) = 1 \ right] = 0 \ End> y_j, [/ math] în cazul în care [matematica] y_j = \ beginx_j, \ textul \ \ arg_j \ stânga [P_t (x_1, x_2, \ ldots, x_n) = 1 \ dreapta] = 1 \\ \ bar_j, \ textul \ \ arg_j \ stânga [P_t (x_1, x_2, \ ldots, x_n) = 1 \ right] = 0 \ end [/ matematica] [matematica] \ arg_j \ stânga [P_t (x_1, x_2, \ ldots, x_n) = 1 \ right] = \ begin1, \ textul \ \ forall (i, l) \ în P_t (x_1, x_2, \ ldots, x_n), \ arg_j (i, l) = 1 0 \\, \ textul \ \ forall (i, l) \ în P_t (x_1, x_2, \ ldots, x_n), \ arg_j (i, l) = 0 \ end [/ math]
Exemple de construcție a MDNF
Construim o hartă Carnot pentru o funcție de trei variabile:
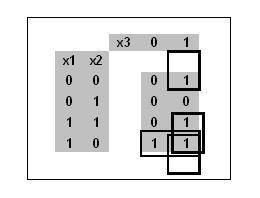
Unitățile din harta Carnot sunt acoperite, în mod minim, de un dreptunghi al formulei 1 × 2 și de două dreptunghiuri din formularul 2 × 1, care corespunde celor trei conjuncții elementare ale celor două argumente. Rețineți că două dreptunghiuri incomplete ale formularului 2 × 1 corespund unui dreptunghi complet al acoperirii.
Construim o hartă Carnot pentru o funcție a patru variabile:
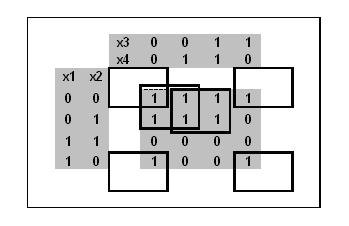
Unitățile din harta Carnot sunt acoperite în mod minim de trei pătrate din formularul 2 × 2, care corespund celor trei conjuncții elementare ale celor două argumente. Rețineți că patru pătrate incomplete de colț corespund unui întreg pătrat al capacului.
Construim o hartă tridimensională Carnot pentru o funcție de cinci variabile:
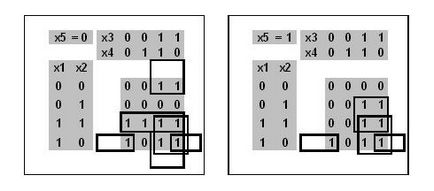
Unități de tri-dimensională Karnaugh hartă paralelipipede minimal acoperite forma 2 x 2 x 2, 2 x 2 x 1 (două), 1 x 4 x 1 x 2 x 1 2, care corespunde unei conjunctie elementare două argumente și patru conjunctie elementare trei argumente. Rețineți că fețele extreme și colțurile sunt combinate.