Definiți mașina zero, infinitatea mașinii și mașina epsilon
A avea încredere în calculul făcut pe computer, fără să înțeleagă exact cum este efectuat acest calcul, este unul dintre cele mai grave lucruri pe care un inginer le poate face în munca sa. Din păcate, experții nu sunt mai puțin frecvenți, ceea ce nu este confundat de rezultatul nonzero obținut prin înmulțirea cu zero sau, invers, cu zero, unde nu ar trebui să fie teoretic zero.
Prin urmare, în această notă, repetăm câteva adevăruri elementare despre reprezentarea numerelor reale într-un calculator și despre regulile de efectuare a operațiunilor cu aceștia.
În calculatorul compatibil cu IBM pentru numere reale, se folosește sistemul binar și se adoptă forma de reprezentare a numerelor în virgulă mobilă ale formularului x = m * 2 p. unde mantisa este m = ± (g1 * 2-1 + g2 * 2-2 + + gt * 2-t). g1. - cifre binare și, g1 = 1. și o valoare întregă p este numită ordine binară. Număr de cifre t. care este alocată pentru înregistrarea mantisei, se numește lățimea mantisei. Intervalul de reprezentare a numerelor în calculator este limitat de lățimea finită a mantistei și valoarea numărului p.
Toate numerele reale x reprezentabile pe un calculator satisfac inegalitățile 0 Toate numerele modulo sunt mai mari decât X∞. nu sunt reprezentate pe un computer și sunt considerate infinite de mașină. Toate numerele care sunt mai mici cu modulul decât X0. Pentru un calculator, acestea nu diferă de zero și sunt tratate ca mașină zero. Mașina epsilon εM este precizia relativă a unui computer, adică limita erorii relative în reprezentarea numerelor reale. Se poate arăta că εM ≈ 2 -t. Fie x * = m * 2 p. Atunci limita erorii absolute a reprezentării acestui număr este δ (x *) ≈ 2 -t-1 * 2 p. Deoarece 1 / 2≤m<1. то величина относительной погрешности представления оценивается как δ(x * ) ≈ δ(x * ) / |x * | ≈ (2 -t-1 *2 p ) / (m*2 p ) = 2 -t-1 / m ≤ 2 -t-1 / 2 -1 = 2 -t. Epsilonul mașinii este determinat de lățimea mantistei și de metoda de rotunjire a cifrelor realizate pe un computer specific. Luăm următoarele metode pentru a determina valorile aproximative ale cantităților necunoscute: Apoi, setăm acest lucru în mediul necesar (pachetul) și selectăm valorile parametrilor, aici este un exemplu pentru MathCAD 15: Ei bine, câteva mențiuni standard în sfârșit: Pentru valorile reale în cazul general, operația == ("comparație") nu este aplicabilă din cauza unei reprezentări inexacte a acestor valori în memoria calculatorului. Prin urmare, pentru variabilele reale, o relație a formei a == b este de obicei înlocuită de fabs (a-b) ≤eps. unde fabs () este o funcție pentru calculul modulului unui număr real, iar eps este o cantitate mică care determină eroarea admisă. Eroarea permisă poate fi de asemenea introdusă în calcul folosind metoda standard de rotunjire rotundă, de exemplu, calculul stâng al produsului numerelor din MathCAD nu dă zero și cel corect - da:
mașină zero, mașină infinit și mașină epsilon în MathCAD 15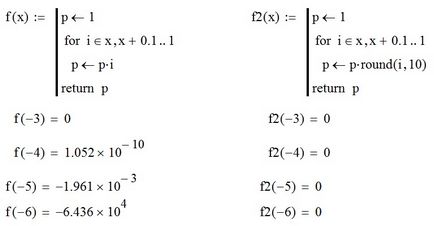
contabilizarea erorilor folosind metoda rotundă (Mathcad)