Există o clasă importantă de ecuații integrale care pot fi rezolvate cu ușurință prin reducerea la un sistem de ecuații algebrice. Astfel de ecuații integrale sunt cu așa-numitele kerneluri degenerate.
Definiție: Se consideră că kernelul unei ecuații integrale este degenerat dacă poate fi reprezentat ca o sumă a unui număr finit de termeni, fiecare dintre acestea fiind rezultatul a două funcții, primul dintre ele depinzând doar de x, iar al doilea doar de x # 958;:
Presupunem că ambele sunt continue pe [a, b] și că, și ele sunt independente liniar între ele.
Ecuația (1) are forma:
Înlocuim (29) în (1):
Deci, cum. sunt liniar independente atunci
Rezolvând sistemul (32), rezolvăm astfel ecuația integrată dată folosind formula (29). Dacă sistemul algebric (32) nu este soluționat, atunci este și ecuația integrală.
D (# 955;) este un polinom de grad ≤ n și D (# 955;) ≠ 0, deoarece # 955; = 0, D (0) = 1. prin urmare, D (# 955;) are ≤ n rădăcini distincte.
D (# 955;) este numit determinantul Fredholm pentru ecuația (1).
1. În cazul în care # 955; este astfel încât D (# 955;) ≠ 0, apoi sistemul (32) și, în consecință, ecuația (1) are o soluție unică definită prin formula (29). În acest caz, pentru f (x) = 0 și deci sistemul (32) are o soluție unică; prin urmare (X) = 0. Asta înseamnă că acestea # 955; pentru care D (# 955;) ≠ 0, nu este o valoare proprie.
Concluzie. În cazul în care # 955; nu este o valoare proprie, atunci ecuația (1) are o soluție unică.
Evident, pentru ca ecuația neomogenă (1) să aibă o soluție unică pentru orice f (x) (
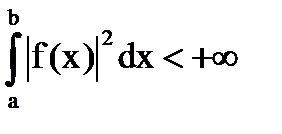
Notă: Ca regulă, atunci când rezolvăm ecuațiile integrale, trebuie adesea să recurgem la metode aproximative. Este important să se stabilească solvabilitatea ecuației pentru orice parte dreaptă (folosind prima teorema). Este mai convenabil să se demonstreze că o ecuație omogenă sau o transpunere (conjugat) nu are decât o soluție trivială. Din aceasta, prin Teorema 1, urmează solvabilitatea ecuației neomogene.
Trei teoreme fundamentale ale lui Fredholm privind solvabilitatea ecuațiilor cu kerneluri degenerate pot fi extinse la cazul unui kernel arbitrar continuu.
Găsiți soluția de ecuații cu kerneluri degenerate:
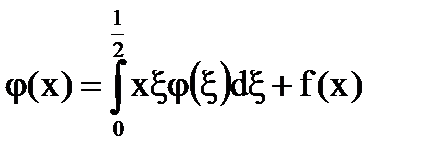
Soluție: Noi denotăm
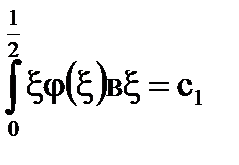
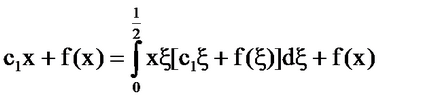
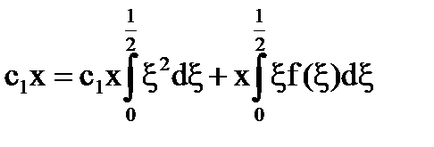
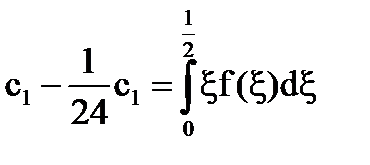
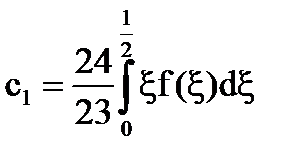
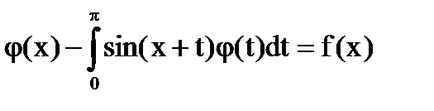
Sistemul [5] are forma:
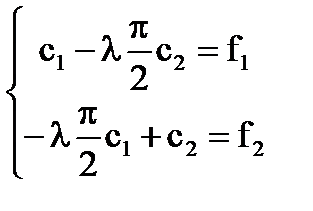
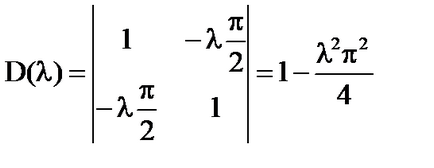
D (# 955;) = 0; ; sunt proprietățile ecuației.
În cazul în care # 955; # 955; atunci D (# 955;) ≠ 0 și sistemul are o soluție unică:
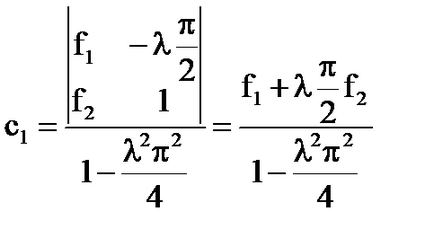
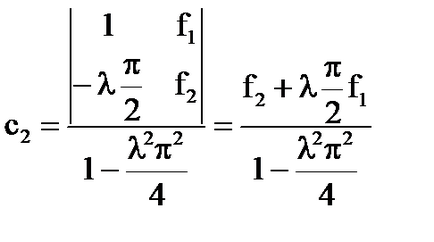
- soluția unică a ecuației integrale
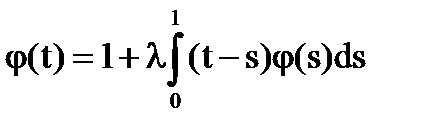
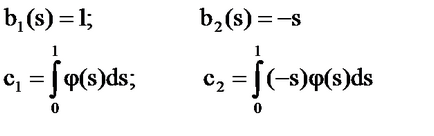
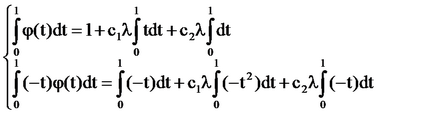
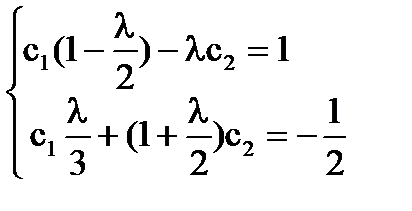
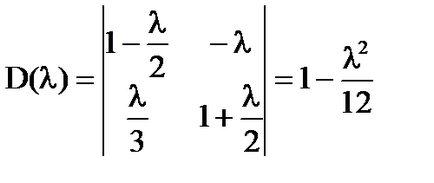
D (# 955;) ≠ 0 pentru orice valoare reală # 955;
Prin formulele lui Cramer;
În cazul în care. apoi soluția unică a ecuației
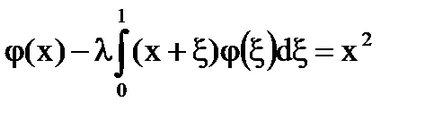
Soluția este: = x + # 958; - continuu în pătratul 0≤x, # 958; ≤1 și este degenerat.
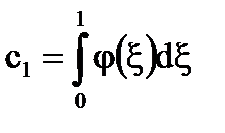
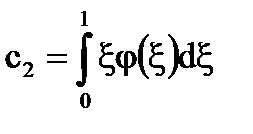
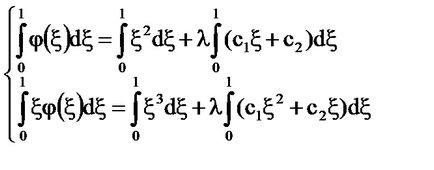
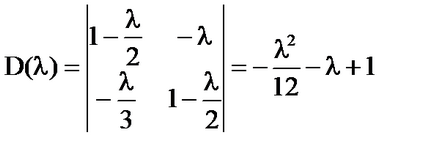
În cazul în care. apoi soluția unică
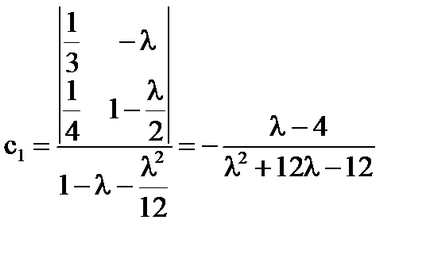
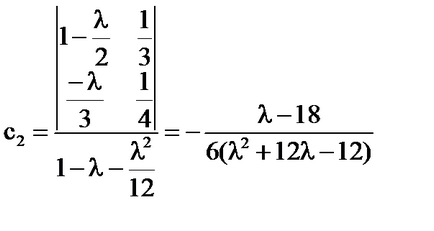
-
soluția unică a ecuației pentru.
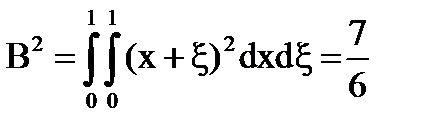
Soluția există, unică și poate fi găsită prin metoda aproximărilor succesive cu
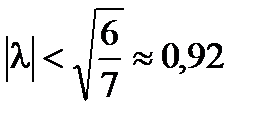
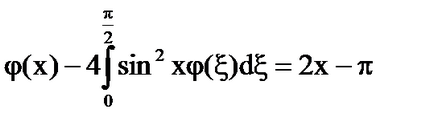
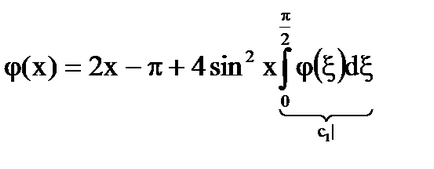
Soluție: kernelul este degenerat.
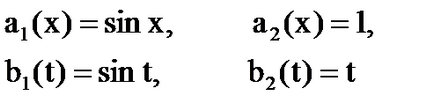
prin formulele [6] - [7] calculăm
Sistemul [5] ia forma
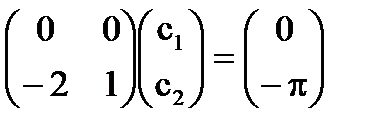
= C, = -π + 2C, unde C este o constantă arbitrară.
Răspuns: Orice funcție a formularului
este o soluție a ecuației integrale date și a altor soluții care nu au această ecuație.
Sarcina pentru munca independenta:
Rezolvați ecuațiile integrale cu nucleele degenerate