Fiabilitate și riscuri
5.1. Definirea conceptului de "risc"
Eșecul sistemului tehnic duce în mod inevitabil la pierderi: producția se oprește sau scade, sistemul eșuat are nevoie de reparații și consecințele eșecurilor de lichidare. În plus, funcționarea mașinilor poate avea un impact negativ asupra mediului și a oamenilor. Siguranța funcționării mașinilor a devenit una dintre problemele umane reale.
Riscul este un atribut inevitabil al funcționării mașinilor. Este unul dintre cei mai importanți indicatori ai securității. Riscul care decurge din eșecul tehnologiei se numește tehnogenic.
Eșecurile tehnologiei duc la pierderi. Tipul și mărimea pierderilor depind de tipul și condițiile de defectare. De exemplu, eșecul motorului de aeronavă în parcare și în zbor duce la pierderi complet diferite. Pierderile, ca eșecurile, sunt evenimente aleatorii, iar dimensiunea pierderii este o valoare aleatorie.
Riscul se referă la posibilitatea pierderilor datorate anomaliilor interne din sistem sau anomaliilor mediului.
Riscul tehnologic este posibilitatea pierderilor datorate defecțiunilor echipamentului.
Riscul poate fi considerat ca fiind probabilitatea apariției unor evenimente adverse, dar mai des la risc, să înțeleagă efectele nocive estimate (pierderi) de la evenimentele adverse. În cele mai multe cazuri, riscul este estimat de unitățile monetare, deși pot exista și alte cazuri. De exemplu, atunci când se exploatează o centrală nucleară, riscul poate fi estimat ca cantitatea de substanțe radioactive care pot părăsi reactorul.
Evaluarea riscului provocat de om. Riscul cumulativ provocat de om
Fie p probabilitatea unui eveniment nefavorabil, de exemplu, eșecul sistemului și c este valoarea pierderilor rezultate din eșec. Apoi pierderea medie sau riscul mediu se calculează după formula:
Acum, ia în considerare un sistem care poate lua state, numerotate de la unul la m. Aceste stări sunt împărțite în două subseturi disjuncte: - setul de stări favorabile și - setul de stări nefavorabile.
Mai întâi, vom presupune că este imposibil să revenim dintr-o stare nefavorabilă la o stare favorabilă.
Fie probabilitatea ca sistemul să rămână în starea j-th, cantitatea de pierdere atunci când atinge această stare. Vom presupune că valoarea nu depinde de tranziția concretă prin care sistemul a căzut într-o stare nefavorabilă.
În figură, stările favorabile corespund cercurilor, pătratele sunt nefavorabile. Folosind formula de probabilitate completă, obținem o expresie pentru riscul tehnogenic mediu al sistemului la un moment dat.
Luați în considerare aplicarea acestei formule la exemplul unui sistem non-redundant care nu este redundant de două elemente. Diagrama stărilor acestui sistem va arăta astfel:
Condiții: 0 - toate elementele sunt în stare de funcționare 1 - eșecul elementului 1, pierderea; 2 - eșecul elementului 2, pierderea.
Probabilitatea de a fi în statele 1 și 2 va fi:
Riscul va fi
Din această formulă se poate observa că riscul crește cu timpul de la zero la maxim (realizat cu timpul care tinde spre infinit). Să presupunem că există un anumit risc. peste care ne putem permite să folosim un sistem tehnic. Să găsim timpul maxim permis pentru utilizarea sistemului:
Această abordare este potrivită pentru descrierea riscului în sistemele nerecuperabile în care sistemul nu poate ieși din starea defecțiunilor și pierderile nu se acumulează în timp. Dacă sistemul este restabilit, atunci după o defecțiune poate fi restaurat și apoi din nou merge într-o stare nefavorabilă. Ca rezultat, riscul total al sistemului se va acumula în timp. Un astfel de risc se va numi risc cumulativ sau acumulat.
Să ne amintim legătura dintre probabilitatea găsirii unui sistem în stare și numărul mediu de tranziții exprimate de formula.
- numărul mediu de tranziții de la statul i la cel j. Pierderile pot apărea dacă tranziția de la o stare favorabilă la o stare nefavorabilă sau dintr-o stare nefavorabilă la alta. Indicăm prin pierderea care apare în fiecare astfel de tranziție. Pierderile medii pe care le vom avea ca urmare a transferului vor fi egale:
Apoi pierderile totale medii se calculează după următoarea formulă:
În cazul particular în care funcționarea sistemului este descrisă printr-un proces aleator Markov:
De exemplu, să luăm întregul sistem non-redundant, dar acum să presupunem că este recuperabil:
Condiții: 0 - toate elementele sunt în stare de funcționare 1 - eșecul elementului 1, pierderea; 2 - eșecul elementului 2, pierderea.
Rezultatele calculării probabilităților de stări adverse și de riscuri sunt prezentate în următoarele diagrame.
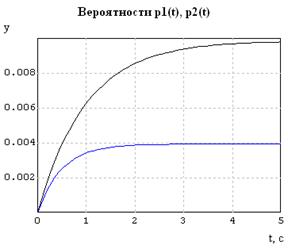
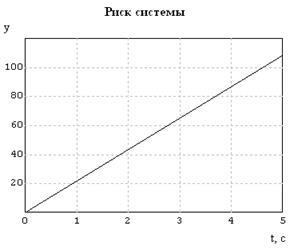
Orice sistem creat de om trebuie să ofere un efect (câștig) din funcționarea sa, adică ar trebui să fie util. Beneficiile utilizării tehnicii pot fi de natură diferită și sunt măsurate în diferite unități. Deseori, luați în considerare efectul economic al utilizării sistemului și câștigul este măsurat în unități monetare.
Utilitatea sistemului tehnic în timpul funcționării acestuia poate fi estimată prin "câștigul" W (t) pe care sistemul îl aduce în timp t. Câștigul total al sistemului constă în câștigul șederii sistemului în stările de câștig și al câștigului care rezultă din tranzițiile instantanee de la stat la stat.
Denumim prin câștigul obținut pe unitate de timp din șederea sistemului în starea i. Dacă starea i este defectă, va fi o valoare negativă și poate fi considerată drept o pedeapsă de reparație, simplă etc.
Similar cu tranziția de la starea i la cea de-a treia, se poate compara numărul - câștigul sau pierderea printr-o tranziție.
Plata medie, datorată șederii sistemului în starea i, va fi egală cu produsul în funcție de timpul mediu al șederii sistemului în această stare. Câștigul mediu datorat tranzițiilor de la starea i la starea j va fi egal cu produsul după numărul mediu de tranziții. Atunci câștigul total al sistemului în timp t este egal cu:
Formula anterioară obținută de risc cumulativ din utilizarea sistemului este un caz special al formulei câștigătoare primite.
Calculăm câștigul pentru sistemul considerat mai sus în următoarele ipoteze:
De asemenea, ia în considerare modul în care fiabilitatea va afecta câștigurile. Pentru a face acest lucru, calculați câștigurile pentru următoarele trei cazuri:
- fiabilitate normală:
- fiabilitate redusă:
- fiabilitate redusă: