Necesitatea de a calcula aria diferitelor figuri, inclusiv triunghiulare, a apărut cu câteva secole înainte de epoca noastră. Oamenii de știință și astronomii s-au gândit la acest lucru în Egiptul antic.
În viață, uneori există situații când trebuie să se uite în coșurile de cunoștințe de memorie din anii școlari îndepărtate: repararea toate au venit în casă și au nevoie pentru a calcula cantitatea de material necesar, sau trebuie să cunoască suprafața de teren sub forma unui triunghi.
Memoria omului nu poate reproduce imediat cunoștințele școlare inutile, ceea ce este destul de natural. Prin urmare, aici sunt colectate principalele metode de calcul al zonei celor mai multe tipuri de triunghi.
Calculați suprafața unui triunghi poate fi variantă variată, aplicând anumite formule. Metodele de calcul depind de tipurile de forme triunghiulare și de ceea ce sunt cunoscute datele computaționale.
Triunghi: definiție și tipuri de forme
Din cursul geometriei se știe că un triunghi este o figură poligonală care are trei puncte pe diferite linii legate de segmente. dimensiune suprafață triunghi exprimată prin numărul de unități închise în pătrate, și este un număr pozitiv care indică dimensiunea figurii, în parte a suprafeței delimitate de cele trei segmente într-o buclă închisă.
În funcție de lungimea laturilor și a unghiului, se disting mai multe soiuri de triunghiuri:
- rectangular, având un unghi drept;
- Angulare, toate unghiurile fiind ascuțite, adică mai puțin de 90 de grade;
- Obtuse, care conțin un unghi obtuz în intervalul de la 90 la 180 de grade;
- isoscele, cu două laturi laterale egale;
- Echilateral, în care toate cele trei părți au aceeași valoare.
Pentru a calcula suprafața fiecărui tip de formă triunghiulară, se folosește o formulă specială.
Cum se calculează suprafața unui triunghi?
Formulele clasice pentru calcularea ariei figurilor triunghiulare corespund tipurilor de triunghiuri. Următoarele formule pentru determinarea zonei unui triunghi arbitrar sunt potrivite pentru stabilirea zonei, indiferent de caracteristicile, unghiurile sau dimensiunile acesteia.
Dreptunghiular triunghi
Un triunghi cu unghi drept este caracterizat de un unghi drept. Două dintre laturile sale, formând acest colț, se numesc catetețe. Spre deosebire de unghiul drept, partea triunghiului se numește hypotenuse.
Formula de bază pentru calcularea ariei unui triunghi dreptunghiular se bazează pe valorile picioarelor din figură.
unde a, b sunt picioarele triunghiului.
- Valorile celor două picioare sunt multiplicate.
- Valoarea obținută este împărțită în două.
Calculați aria unui triunghi în unghi drept cu o altă formulă, în care valoarea ipotezei și înălțimea atrăgătoare sunt luate ca bază.
unde c este hypotenuse, hc este înălțimea față de hypotenuse.
- Lungimea hipotenentei este înmulțită cu înălțimea de la vârful opus.
- Valoarea rezultată este redusă la jumătate.
Triunghiul izoscel
Într-un triunghi isoscel, cele două laturi laterale sunt egale în valoare, partea diferită dimensional se numește bază.
Suprafața unui triunghi isoscel este calculată prin formula:
unde a sunt laturi egale ale triunghiului, b este baza.
- Diferența este determinată de rădăcina pătrată pătrată pe laturile egale și rădăcina pătrată a bazei.
- Din valoarea obținută, se extrage rădăcina pătrată.
- Rezultatul este înmulțit cu valoarea bazei, redus de 4 ori.
Triunghi echilateral
Un caz special al unui triunghi isoscel este unul echilateral, diferit prin faptul că toate laturile și unghiurile figurinei sunt egale în valoare.
Suprafața unui triunghi echilateral este determinată de formula:
unde a este partea unui triunghi echilateral.
Determinarea ariei unui triunghi cu date necunoscute
Formulele clasice pentru calcularea ariei unui triunghi nu pot ajuta întotdeauna. Există o serie de situații în care cantitățile necesare pentru substituția din formula sunt necunoscute. Alte metode sunt utilizate pentru a calcula aria triunghiului, în funcție de datele cunoscute. Toate opțiunile prevăd o formulă specifică și o anumită procedură pentru efectuarea calculelor.
Baza și înălțimea cunoscute
Zona triunghiului este definită ca jumătate din produsul înălțimii figurii și lungimea bazei, adică partea acelui triunghi la care este înălțată înălțimea.
unde b este lungimea bazei; h este înălțimea.
- Multiplicați înălțimea cu lungimea bazei, obținem aria poligonului.
- Pentru a obține zona unui triunghi, rezultatul este împărțit la 2.
Valorile celor trei laturi sunt cunoscute
Zona triunghiului este calculată prin formula lui Heron. Pentru a facilita formula, metoda implică un calcul preliminar al valorii semiperimetrice.
unde p este valoarea semiperimetrică; a, b, c sunt lungimile laturilor triunghiului.
- Calcularea unui semiperimetru prin formula
- Calculul suprafeței figurii conform formulei lui Heron.
Există două laturi și unghiul dintre ele
Zona triunghiului se calculează ca fiind produsul a două laturi înmulțit cu sinusul unghiului situat între aceste laturi. Unghiul este o figură geometrică obținută din două raze care provin dintr-un punct (vârful colțului).
unde a, b sunt laturile triunghiului, C este unghiul dintre laturi.
- Înmulțirea a două laturi.
- Definiția sinusului unui unghi este o funcție trigonometrică, într-un triunghi cu unghi drept, egal cu raportul dintre piciorul opus și hypotenuse.
- Înmulțirea produsului din două laturi cu unghiul sinusului.
- Rezultatul este împărțit în jumătate.
O latură este cunoscută și unghiurile adiacente acesteia
Suprafața acestui triunghi este egală cu jumătate din pătratul unui anumit aspect, înmulțit cu o fracție cu numărătorul care exprimă produsul de sinusul colțuri adiacente, iar numitorul indicând sinusul unghiului opus.
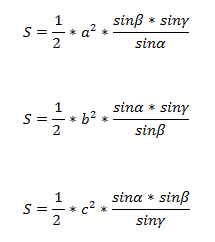
- Pătratul laturii cunoscute este calculat și împărțit la 2.
- Sinusurile colțurilor adiacente sunt înmulțite și împărțite în sinele opusului. Un unghi opus se calculează prin formula:
- Valorile obținute sunt multiplicate.
Raza cercului inscripționat și semiperimetrul sunt cunoscute
Suprafața unui triunghi este definită ca fiind produsul razei cercului inscripționat prin semiperimetrul său. Se spune că un cerc este inscripționat dacă are un punct comun cu poligonul de pe fiecare parte a figurii. Punctul central al unui cerc înscris într-un triunghi este întotdeauna localizat în punctul în care se intersectează bisectoarele unghiurilor sale interne.
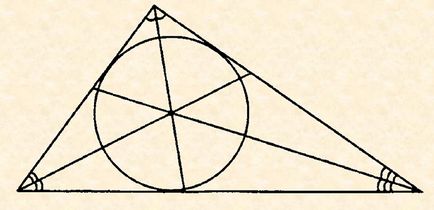
S = p * r, unde p este semi-perimetrul triunghiului, r este raza cercului înscris.
1. Semi-perimetrul este definit ca jumătate din suma tuturor laturilor triunghiului conform formulei:
unde a, b, c sunt laturile triunghiului.
2. Se înmulțește semiperimetrul triunghiului și raza cercului inscripționat.
Raza cercului circumscris și perimetrul
Un triunghi este numit circumscris în jurul unui cerc, dacă părțile sale atinge cercul, iar el însuși este în afară. Suprafața unui triunghi este definită ca jumătate din produsul perimetrului triunghiului și a razei cercului circumscris.
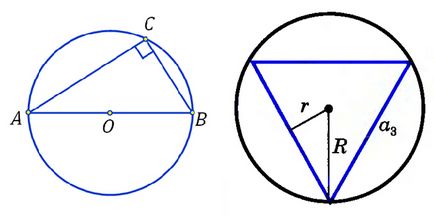
unde r este raza cercului circumscris, a, b, c sunt laturile triunghiului.
- Perimetrul unui triunghi este definit ca suma tuturor laturilor sale.
- Raza cercului circumscris este înmulțită cu perimetrul triunghiului.
- Rezultatul este împărțit în jumătate.
Cunoașterea formulelor de calcul aria triunghiului ajută la determinarea ariei figurilor tridimensionale, bazate pe fețele care sunt forme triunghiulare, cum ar fi, de exemplu, o piramidă.