Într-o rețea de curent alternativ, etc cu. iar tensiunea trebuie să varieze în conformitate cu legea armonică, adică ele trebuie să fie sinusoidale. Abaterile de la forma sinusoidală a tensiunii din rețeaua AC conduc la pierderi suplimentare de energie.
Luați în considerare generarea unui curent alternativ sinusoidal cu rotație uniformă a cadrului într-un câmp magnetic omogen. Lăsați cadrul ABCD, ale cărui capete sunt conectate la inelele metalice, să se afle într-un câmp magnetic omogen cu inducția B (figura 26.1, a). La inele, periile și b sunt conectate, conectate la consumatorul de energie electrică. Dacă cadrul este rotit în jurul axei OO1 în sensul acelor de ceasornic cu o viteză unghiulară constantă ω, atunci în lungimile firelor AB și CD va apărea. etc cu. inducția e1 și e2, egală în mărime și opusă direcției.
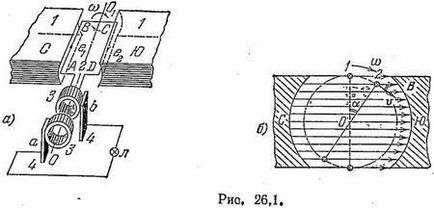
Mișcarea firelor AB și CD va avea loc de-a lungul unui cerc cu diametre d = AD și cu o viteză liniară v = ωd / 2. Dacă timpul și unghiurile sunt citite din poziția cadrului 1 din Fig. 26.1, b, atunci unghiul de rotație al cadrului α este exprimat prin formula:
α = ωt sau α = 2πt / T, (26.1)
unde T este timpul unei revoluții complete a cadrului. Deoarece unghiul α este egal cu unghiul dintre vectorii B și V, pentru e. etc cu. Inducția în segmentul AB sau CD avem formula:
unde l este lungimea conductorului AB sau CD. Rețineți că astfel de conductoare sunt numite active, deoarece atunci când conturul este rotit, numai în ele este emitentul indus. etc cu. Generalități e. etc cu. în cadrul cu aceasta:
e = 2e1 = 2vlB sin α, sau e = 2 (ωd / 2) lB sin ωt.
Astfel, atunci când cadrul este rotit uniform într-un câmp magnetic uniform, e este indusă în el. etc cu. definite prin formula:
e = ωdlB sin ωt sau e = ωdlB sin (2πt / T). (26.2)
Deoarece ω, d, l și B sunt constante, produsul lor poate fi notat cu o singură literă ξm, adică ξm = ωdlB. apoi:
e = ξm sin ωt sau e = ξm sin (2πt / T). (26.3)
Amintiți-vă că valoarea maximă a sinusului este una. În consecință, ξm în formula (26.3) denotă valoarea maximă emf. etc cu. Acesta din urmă apare în cadru pe măsură ce acesta se rotește; ξm se mai numeste si amplitudinea e. etc cu. Graficul unei variabile sinusoidale e. etc cu. este prezentat în Fig. 26,2. Rețineți că valorile instantanee pentru AC sunt de obicei indicate cu majuscule și valorile maxime, în amplitudine, cu majuscule. De exemplu, pentru intensitatea curentului instantaneu, notația i este utilizată, iar pentru valoarea amplitudinii Im. Stresurile reprezintă u și Um.
În acest exemplu, circulară (ciclic) ω frecvență AC în formulele (26.2) și (26.3) coincide cu viteza unghiulară de rotație a domeniului de aplicare într-un câmp magnetic și modifică perioada AC T coincide cu perioada de rotație a cadrului. Rata de recurență a modificărilor în curent alternativ este caracterizată de o frecvență v:
Prin urmare, formula (26.3) poate fi scrisă după cum urmează:
e = ξm sin2πvt (26.3a)
Dacă numărul de rotații ale cadrului pe minut este notat cu n, atunci:
Frecvența tehnică standard a curentului alternativ în URSS este de 50 Hz. Aceasta înseamnă că e. etc cu. iar curentul își schimbă direcția în circuit de 100 de ori pe secundă. Acest curent este referit la curenții de joasă frecvență. În scopuri speciale, curenții sunt utilizați, a căror frecvență atinge milioane de hertzi. Se numesc curenți de înaltă frecvență.