UNCERTAINTY INTEGRAL "
curs de matematică superioară la Facultatea de Chimie
Scopul studierii temei "Integrala indefinita" la Facultatea de Chimie este mastering de catre studenti a metodelor de baza de calcul al integrelor indefinite. Specificitatea studierii acestui subiect este că, în esență, are un accent practic: principala atenție este acordată descrierii algoritmilor pentru găsirea de integrale de tipuri standard. În acest sens, aceste linii directoare oferă un număr mare de exemple caracteristice care ilustrează metodele de bază de calcul al acestor integrale. De asemenea, luăm în considerare greșelile tipice făcute de studenți.
1. Primitiv. Integralul indefinit.

2. Tabelul integralelor.


4. Înlocuirea unei variabile într-o integritate nedeterminată.
Una dintre principalele metode de integrare a funcțiilor este metoda de modificare a unei variabile. Se bazează pe următoarea considerație. Dacă se știe acest lucru


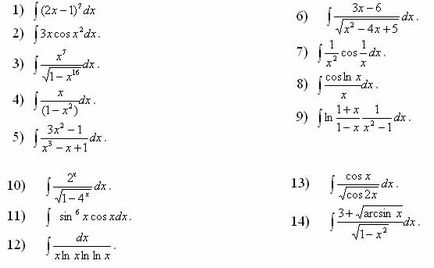
5. Integrarea pe părți.
Fie u (x) și v (x) funcții diferențiate. Formula pentru integrarea prin părți are forma:

Formăm regula pentru rezolvarea exemplelor prin metoda integrării prin părți:
1) În integrand, selectăm partea diferențiabilă (u) și partea integrabilă (dv), folosind recomandările 1 și 2.
2) Găsiți du, diferențiând u.
3) Găsiți v prin integrarea dv.


Găsiți următoarele integrale:

6. Integrarea într-o formă finită.
După cum se știe, derivatul oricărei funcții elementare, la rândul său, este o funcție elementară. Situația este diferită cu integralele: integramentul nu depinde de nici o funcție elementară în termeni de funcții elementare. De exemplu, se știe că integralele

nu poate fi exprimată în termeni de funcții elementare.
Dacă integrarea unei funcții elementare este exprimată în termeni de funcții elementare, atunci spunem că funcția dată este integrată într-o formă finită. O clasă importantă de funcții integrabile într-o formă finită este clasa funcțiilor raționale.
7. Integrarea fracțiunilor raționale.


Integrarea celor mai simple fracții de tipurile 1 și 2 se reduce la integralele de masă 4 și 3. Noi integram o fracțiune de tip 3. Avem


După aceea, rămâne să se integreze cele mai simple fracții și să se combine rezultatele.

Găsiți următoarele integrale.

8. Integrarea celor mai simple iraționalități.
8.1. Luați în considerare un element integrat al formei




