- studiul principiului funcționării pendulului balistic și a legii de conservare a momentului unghiular;
- verificarea experimentală a dependențelor dintre cantitățile fizice care caracterizează oscilațiile torsiunii;
- determinarea experimentală a forțelor torsionale elastice constante și a momentului de inerție al pendulului balistic;
- determinarea experimentală a vitezei bulletului cu ajutorul unui pendul balistic.
Dispozitive și accesorii:
- pendulul balistic GRM-02 cu contor de timp automat, milisecundometru și dispozitiv de fotografiere.
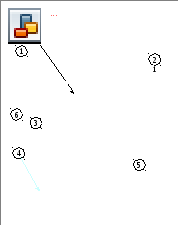
Figura 1 - Vedere generală a instalației GRM-02
Instalația constă din:
1) pendulul balistic (1), suspendat pe un filet de oțel. Pendulul este alcătuit din două tije de oțel amplasate diametral, de-a lungul cărora se pot mișca masele. Pe una din tije este fixată o țintă plină cu lut;
2) dispozitivul de fotografiere (2);
3) senzor fotoelectric (3);
4) contorul automat al numărului de perioade (4);
5) milisecundă automată (5);
6) a scării unghiulare (6).
Instalația permite măsurarea directă a următoarelor valori: perioada de oscilație a pendulului balistic; amplitudinea unghiulară a oscilațiilor torsionale ale unui pendul balistic.
Pregătirea instrumentului pentru funcționare și măsurare
Aparatul este pornit de butonul "NETWORK". Poziția de echilibru a pendulului balistic este setată astfel încât să corespundă scării unghiulare zero.
Măsurarea perioadei de oscilație a unui pendul balistic.
Montați mărfurile la o distanță R1. sugerată de profesor. Resetați citirea instrumentului apăsând butonul "RESETARE", înclinați ușor pendulul balistic la unghiul stabilit de instructor din poziția de echilibru și eliberați-l. Când pendulul balistic ajunge la numărul de oscilații "nouă" (9), apăsați butonul "STOP". În acest caz, numărul de ore se oprește după zece fluctuații complete. Perioada de oscilație este egală cu timpul împărțit la numărul de oscilații (N = 10). T = t / N.
Măsurarea amplitudinii unghiulare cu un impact absolut inelastic al glonțului asupra țintei de la pendulul balistic plasticinic.
Setați bunurile mobile în poziția propusă (conform indicațiilor instructorului). Încărcați unitatea de arc de încărcare cu un glonț special astfel încât, după comprimarea arcului, acesta să fie fixat și ținut. Un pendul balistic cu o țintă plastilină trebuie să se afle într-o stare liniștită care corespunde poziției zero a scalei unghiulare. Prin apăsarea obturatorului dispozitivului de fotografiere, înregistrați unghiul maxim la care sa abătut pendulul balistic.
După împușcare, glonțul ar trebui să fie blocat și să rămână în țintă plastilină. Această experiență este considerată de succes. În cazul în care glonțul a decolat, instalarea ar trebui să fie resetată și experiența repetată.
Ideea balistică măsurarea vitezei unui glonț este un glonț care în timpul coliziunii cu viteza unghiulară pendul a pendulului balistic variază destul de considerabil, iar mișcarea unghiulară este nesemnificativă și poate fi neglijată. Firește, această condiție este satisfăcută dacă masa pendulului este mult mai mare decât masa bulletului.
Viteza glonțului este determinată prin măsurarea unghiului de abatere maximă a pendulului după o coliziune inelastică cu glonțul. Procesul de ciocniri inelastice cu pendulul descrie un glonț bazat pe legea conservării momentului cinetic (în acest proces de energie mecanică nu este conservată!), Iar procesul ulterior de mișcare poate fi descrisă de legea de conservare a energiei mecanice.
Cu toate acestea, orice model teoretic este doar o descriere aproximativă a situației fizice, deoarece neglijează influența multor efecte care apar în experiment. Dar dacă efectele reale de neglijare în modelul teoretic nu se schimba rezultatul final cu mai mult de 1/20 din valoarea sa reală, atunci acest model teoretic în laborator fizic este Practică destul de acceptabil și vă permite să definiți cantitatea fizică dorită.
În cazul nostru, neglijăm mica deplasarea centrului pendulului de masă după coliziune cu glonțul, vibrațiile elastice, care, astfel apar și, în consecință, redistribuirea energiei mecanice între oscilațiile elastice și torsiune. De asemenea, ia în considerare vibrațiilor de torsiune neamortizate, neglijând rezistența aerului și disiparea energiei vibrațiilor inelastice în sol elastic umeraș de sârmă și așa mai departe. N. Cu toate acestea, modelul teoretic propus permite să obțineți rezultate destul de bune.
Sarcina 1. Determinarea momentului de inerție al pendulului balistic (Io) și a coeficientului forțelor de torsiune elastice (C).
1. Setați greutățile mobile cu o masă M la aceeași distanță d1 de axa de rotație. După ce a respins pendulul balistic cu un unghi φ
20 °, măsurați perioada de oscilație T1. Repetați experimentul de 3 ori și calculați valoarea medie a lui T1.
2. Setați poziția greutăților mobile ale masei M la o distanță d2 și repetați experimentul (vezi sarcina 1). Este mai bine dacă valorile d1 și d2 diferă cât mai mult posibil.
3. Din sistemul de ecuații 1) și 2), înlocuind valorile numerice ale T1. T2. d1. d2. găsi Io și C.
4. Calculați eroarea relativă în determinarea momentului de inerție și a coeficientului forțelor de torsiune elastice
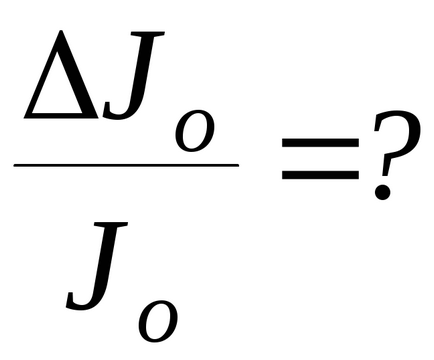
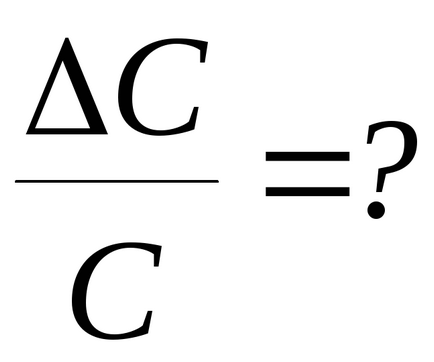
Din cauza complexității expresiei matematice pentru determinarea acestei erori, puteți utiliza o versiune simplificată a calculului. Pentru a face acest lucru, se presupune că erorile relative ale cantităților determinate direct (M, d, T) sunt egale cu:
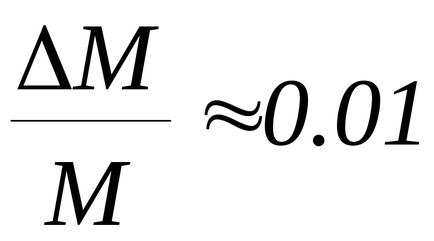
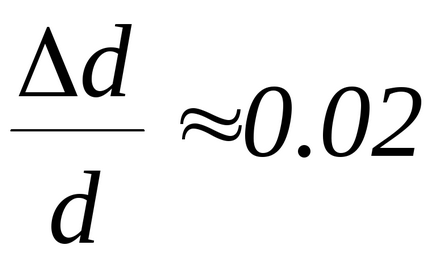

Încărcați dispozitivul de fotografiere și, prin fixarea bunurilor mobile (M) la aceeași distanță d3. face o fotografie, măsurând abaterea maximă a pendulului balistic φmax și distanța de la axa de rotație la centrul de masă al glonțului
Legea conservării momentului unghiular oferă:
unde Vn este viteza glonțului,
Legea conservării energiei mecanice:
Din sistemul de ecuații 3) și 4) găsiți și Vn. Unghiul φmax trebuie înlocuit în radiani:
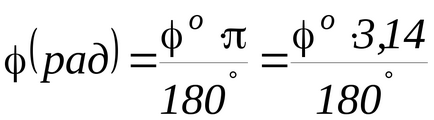
unde φ o este unghiul în grade.
Calculați erorile relative ale vitezei glonțului
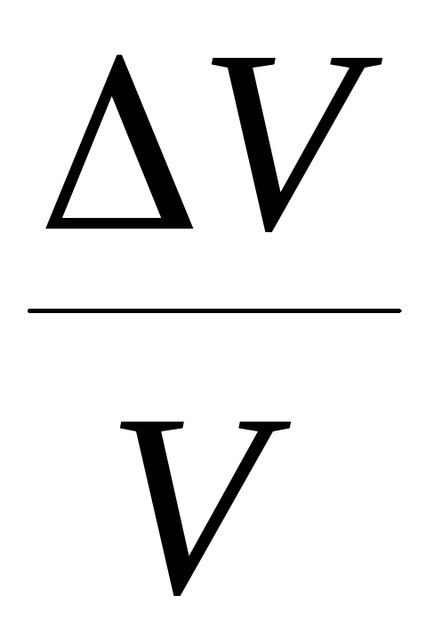
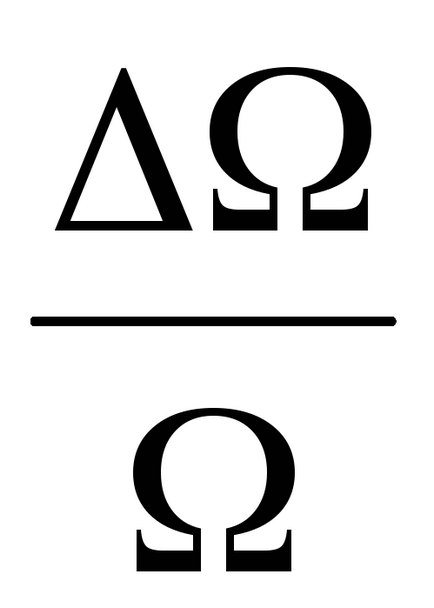
Erorile relative ale cantităților determinate direct (m. Φm.
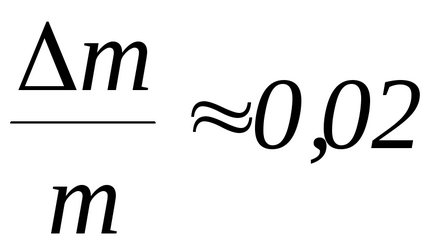
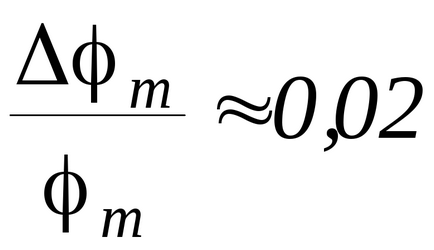
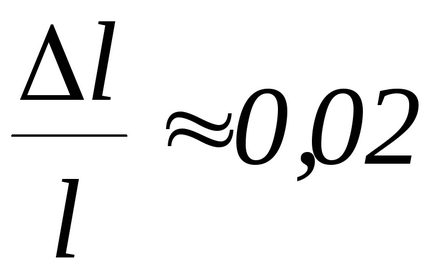
Aplicație. Determinarea vitezei unui glonț de un pendul balistic (material teoretic)
Când te-a lovit un glonț la țintă cu plastilina, pendul balistic dobândește viteza unghiulară și părăsește poziția de echilibru, oscilând în jurul axei sale. Se presupune că viteza glonțului în momentul coliziunii este perpendiculară pe axă și pe brațul pendulului. Dacă această condiție nu este îndeplinită, atunci în plus față de rotație, va fi, de asemenea grade excitat și de vibrație de libertate a pendulului, adică. E. Axa pendulului va începe să oscileze.
Deoarece viteza glonțului este perpendiculară pe planul țintă, momentul impulsului bulletului este egal cu:
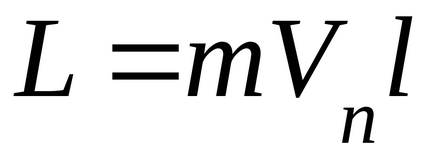
unde
Momentul unghiular al sistemului după coliziune este dat de:
unde eu sunt momentul inerției sistemului după o lovitură de glonț, egală cu: I = Io + 2M
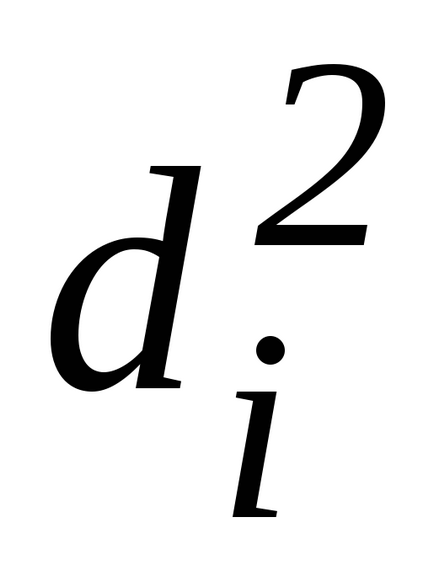
este viteza unghiulară a sistemului după impact.
Impactul poate fi considerat absolut inelastic, deoarece atunci când o țintă atinge ținta, glonțul se blochează în lut. În acest caz, legea conservării momentului unghiular ia forma:
Astfel, după coliziune, pendulul balistic dobândește viteza unghiulară . Când pendulul se mișcă, momentul de forță datorat deformării torsiunii firului de oțel al suspensiei pendulului va acționa asupra acestuia, care este egal cu:
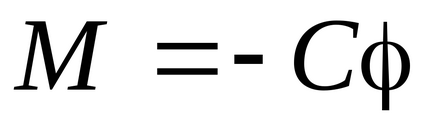
unde C este constanta fortelor elastice de torsiune ale firului;
φ este unghiul de deviere a pendulului din poziția de echilibru.
Semnul minus indică faptul că pentru φ> 0, M <0. Поэтому в момент соударения угловая скорость будет максимальной, а в дальнейшем она будет уменьшаться до нуля.
Cu o mișcare suplimentară, dacă rezistența aerului nu este luată în considerare, legea conservării energiei mecanice este îndeplinită. În momentul deviației maxime, viteza unghiulară este zero, iar energia potențială este maximă și egală cu
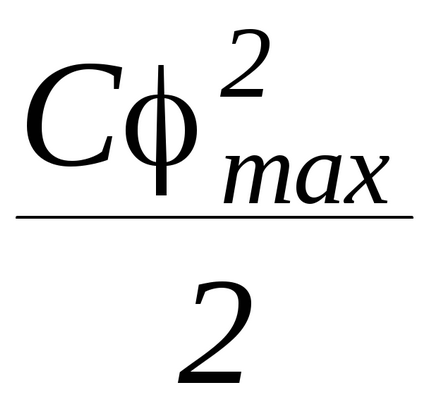
Astfel, putem scrie legea conservării energiei în forma:
unde φmax este unghiul maxim de rotație al pendulului.
Folosind conservarea momentului angular (P-1) și a energiei (P-2), obținem:
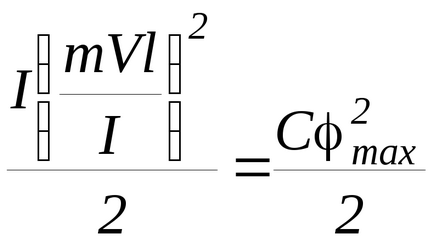
Adică viteza glonțului înaintea coliziunii cu pendulul balistic va fi determinată de expresia:
Dați definiția impulsului unghiular. Cum se utilizează această valoare în munca de laborator?
Care este principiul balistic?
Ce legi de conservare au fost folosite în această lucrare?
Dați definiția momentului de inerție.
Menționați teorema lui Steiner-Huygens.
Cum să determinăm momentul inerției unui pendul balistic?
Cum se modifică unghiul de deviere a pendulului balismatic când acesta se ciocnește cu gloanțele și cu perioada de oscilații, dacă se mărește momentul de inerție?
Ce se întâmplă dacă glonțul atinge un unghi față de planul perpendicular al țintei?
Obțineți o formulă pentru determinarea vitezei glonțului dacă pendulul balistic se abate cu un unghi maxim φ după un impact inelastic.