Acasă> Tutoriale> Ecuatii diferentiale ordinare.> Soluția de ecuații liniare neomogene cu coeficienți constanți și chastyu.1 drept special.
Solutia ecuațiilor liniare neomogene cu coeficienți constanți și chastyu.1 drept special.
Deci, cum să rezolve ecuații diferențiale omogene cu coeficienți constanți, ne-am dat seama în articolul precedent. Luați în considerare în cazul în care partea dreaptă este non-zero, iar o formă specială.
Să considerăm ecuația de forma:
.
Apoi, soluția acestei ecuații va consta din două părți: a. unde - soluția generală a ecuației omogene, și - o soluție particulară a ecuației neomogene.
Să presupunem că partea dreaptă are. unde - polinom de gradul n, atunci forma generală a unei soluții particulare a ecuației neomogene este: unde - forma generală a unui polinom de gradul n cu coeficienți nedeterminat, s egală cu multiplicitatea rădăcina ecuației caracteristice. și anume Dacă această rădăcină nu este prezent, atunci.
Coeficienții polinomului se determină prin metoda coeficienților nedeterminați după înlocuirea în ecuația originală.
Exemplul 1.
S-au găsit. soluția generală a ecuației folosind ecuația caracteristică.
atunci
Ne găsim pe partea dreaptă a mediei.
Partea dreaptă are forma :.
Aici - un polinom de gradul întâi, o astfel ecuația caracteristică nu este, de exemplu, .
Apoi, o soluție particulară a ecuației neomogene va arata:
Noi găsim primul și al doilea derivatele de ordinul de această caracteristică și a pus în ecuație originală.
Substitut în ecuația:
Noi echivala coeficienții puterilor corespunzătoare ale x în diferite părți ale (metoda coeficienților nedeterminați:
Și soluția specială are forma:
Scrieți un răspuns:
răspundă:
Exemplul 2.
Noi găsim soluția generală a ecuației folosind ecuația caracteristică.
Am primit rădăcina reală a multiplicitatea 2.
atunci
Ne găsim pe partea dreaptă a mediei.
Partea dreaptă are forma :.
Aici - un polinom de grad zero, cum ecuația caracteristică la fel de mult la fel de mult ca două, și anume, .
Apoi, o soluție particulară a ecuației neomogene va arăta.
Noi găsim primul și al doilea derivatele de ordinul de această caracteristică și a pus în ecuație originală.
Substitut în ecuația:
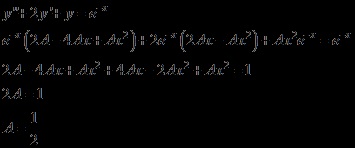
Și soluția specială are forma: