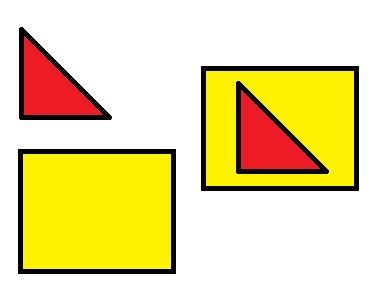
Comparați zone de diferite forme, puteți suprapune metoda. Uită-te la poza. Vedem două forme: un triunghi și un dreptunghi. Pentru a le compara, putem impune o cifră mai mică în cea mare. Triangle complet se potrivesc într-o cutie, înseamnă că triunghiul este mai mică decât dreptunghiul.
Dar nu este întotdeauna posibil să se compare cifrele din zonă în acest fel. Apoi, cifra poate fi defalcate în pătrate egale și contoriza numărul de pătrate incluse în această cifră.
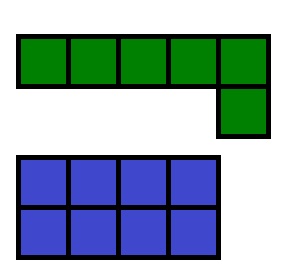
Zona cifra este numărul de pătrate de unități care alcătuiesc această cifră.
În cazul în care o latură pătrat este de 1 cm, atunci suprafața de pătrat este egal cu 1 centimetru pătrat (cm2).
Suprafața unui pătrat o parte care este egală cu 1 decimetru decimetru pătrat (dm 2) sau 100 de centimetri pătrați (cm2).
Suprafața figurii indicate prin litere majuscule S.
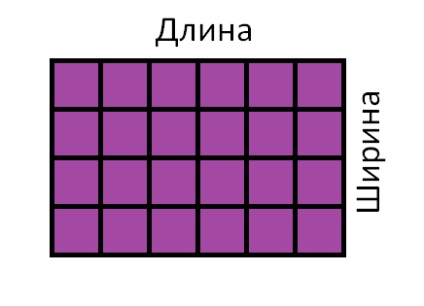
Acum, înmulțiți lungimea dreptunghiului cu lățimea acestuia și pentru a obține zona:
S = 6 × 4 = 24 cm 2
Pentru a calcula aria unui dreptunghi. este necesar să se măsoare lățimea și lungimea sa, în aceleași unități și le găsi locul de muncă.
Dacă știți aria unui dreptunghi și lățime, apoi găsiți lungimea, este necesar să se împartă zona cu o lungime cunoscută.
De exemplu, zona de dreptunghi este de 15 cm 2. Lungimea dreptunghiului este de 5 cm găsi lățimea .:
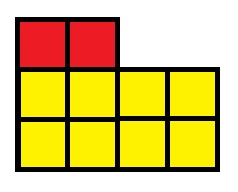
Deci, figura noastră poate fi împărțită în două dreptunghiuri: prima suprafață de 2 cm 2 și o a doua suprafață de 8 cm 2.
S = 2 x 1 + 4 x 2 = 10 cm2
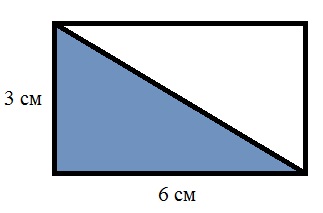
Acum ne găsim aria dreptunghiului care rezultă și împărțiți-l în jumătate:
S = (3 x 6) ÷ 2 = 9 cm 2
Pare simplu, atunci când un triunghi dreptunghiular. În cazul în care triunghiul nu este un unghi drept, apoi se calculează aria sa este după cum urmează:
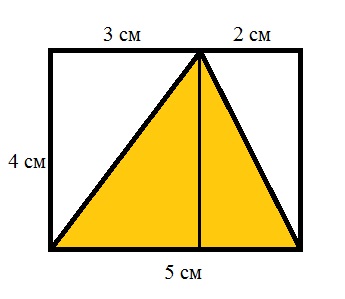
Acum, în scopul de a găsi zona triunghiului nostru, este necesar să se calculeze suprafața celor două triunghiuri unghi drept primite și le-a pus împreună:
S1 = (3 x 4) ÷ 2 = 6 cm 2
S2 = (4 x 2) ÷ 2 = 4 cm 2
S = S1 + S2 = 6 + 4 = 10 cm2