Matricea de transformare este folosită pentru a calcula noile coordonate ale elementului în scopul transformării și permite montarea unei multitudini de transformări simultan. Distinge matrice bidimensional și tridimensional, ele diferă unul de altul în mărime și spațiu, pe care sunt orientate. Deoarece matricea bidimensională sunt mai mici și, prin urmare, mai ușor să se ia în considerare principiul general al matricei pe exemplul său.
matrice bidimensionala
Conversia utilizând o matrice bidimensională are loc în planul ecranului, iar următoarea condiție este aceea că liniile sunt întotdeauna paralele, astfel încât transformarea de rotație permisă, la scară, oblic și schimba poziția, dar nu și perspectiva sau ceva similar. Aceasta este zona de lucru de matrice tridimensională. Fig. 1 prezintă transformările admisibile și imposibil de realizat folosind matrici bidimensionale.
Dar nu fi așa
Fig. 1. Transformarea elementului
Matricea in sine are o dimensiune de 3x3, și în termeni generali scrie:
Pentru simplificare, uneori de-a treia linie este coborâtă, deoarece nu a afectat rezultatul final. Noile coordonate ale fiecărui punct al elementului obținut prin înmulțirea matricei de transformare prin coordonate ale matricei.
Și calculat prin următoarea formulă:
Rolul fiecărei matrice de coeficienți este prezentat în Tabelul. 1.
Tabel. 1. Coeficienții matricei de transformare
Modificarea scalei orizontale. O valoare mai mare de 1 elementul se extinde, este mai mică de 1, invers, se micșorează.
înclinare verticală. O valoare pozitivă se înclină în sus în jos negativ.
înclinare orizontală. O valoare pozitivă se înclină spre stânga, dreapta negativ.
Modificarea scalei verticale. O valoare mai mare de 1 elementul se extinde, este mai mică de 1 - comprese.
Offset în pixeli orizontal. O valoare pozitivă mută elementul spre dreapta printr-un număr predeterminat de pixeli, valoarea negativă este deplasată spre stânga.
Offset pixeli pe verticală. Când elementul pozitiv este redus cu un număr predeterminat de pixeli sus sau în jos, cu o valoare negativă.
Funcția matrice () este folosită pentru transformarea matricei. Coeficienții sunt listate în interiorul paranteze.
matricea identitate
În cazul în care coeficienții de matrice a și d sunt egale cu 1 și elementele rămase ale matricei sunt zero, atunci această matrice se numește o unitate. Această matrice este utilizată în mod implicit, deoarece nu conduce la nici un element de transformare. Deci, dacă aveți nevoie pentru a face doar un singur tip de schimbare, matricea de identitate trebuie să fie luată ca bază.
Scara orizontală
Pentru a mări dimensiunea celulei, să zicem, de două ori pe orizontală, un coeficient trebuie setat la 2, iar coeficienții rămași să părăsească ca o matrice unitate.
Noi credem noile coordonate:
x „= 2 * x + 0 * y + 0
y „= 0 * x + 1 * y + 0
pentru codul prezentat în exemplul 1 de scalare.
Exemplul 1. Scaling
Rezultatul acestui exemplu este prezentată în Fig. 2. Bloc cu text intins cu 20% în direcție orizontală.
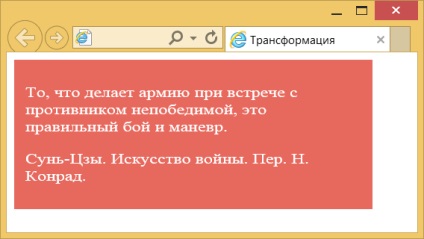
Fig. 2. Modificarea dimensiunii textului
Pentru elementul de reflecție orizontală ar trebui să stabilească o = -1. Vertical d = -1 sau ambele valori simultan la un moment dat pentru a reflecta pe orizontală și pe verticală.
Exemplul 2 prezintă reflexia textului vertical.
Exemplul 2. Reflecția
Rezultatul acestui exemplu este prezentată în Fig. 3.
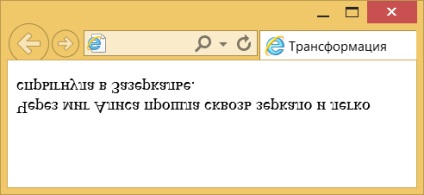
Fig. 3. Reflecție textul pe verticală
Înclinați și de a răspunde coeficienții b și c. și care afectează tipul elementului. Să stabilim c = 1 și a vedea ce transformări sunt obținute.
x „= 1 * x + 1 * y + 0
y „= 0 * x + 1 * y + 0
Astfel, schimbând numai x coordonatei. care este incrementat cu valoarea y. ceea ce duce la elementul de înclinare. Exemplul 3 a folosit o valoare negativă pentru factorul c înclina spre dreapta.
Exemplul 3. Înclinarea
Rezultatul acestui exemplu este prezentată în Fig. 4.
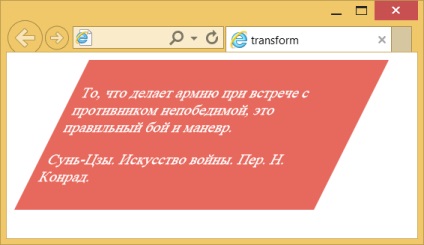
Fig. Unitate 4. Tilt
Rotația este o combinație de scalare și de smoală, dar pentru a menține elementul original, proporțiile de conversie trebuie să se supună strict de calcul folosind sinus și cosinus.
rotație Auto este în sens orar, α definește unghiul de rotație în grade.
deplasare
Pentru elementul de deplasare pe orizontală coeficient de tx responsabil. cât și pe verticală ty. Valoarea servește numărul de pixeli.
matrice tridimensională
Matricea tridimensională având o dimensiune 4x4 si este folosit pentru a coordona elementul de conversie în spațiul tridimensional. În termeni generali, se pare ca acest lucru:
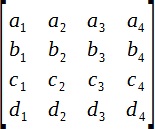
Numele de „tri-dimensional“ reflectă doar faptul că matricea este proiectat pentru a lucra în 3d-spațiu. matrice bidimensionala este un caz special, iar dimensiunile sale 4x4 este următoarea:
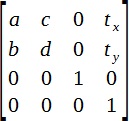
În forma sa pură această matrice este rar folosită datorită complexității lor și prezența unor funcții convenabile pentru spațiu de transformare. Dacă sunteți interesat în trigonometrie și coordonează formulele de transformare alte, apoi citiți acest material.