Există un mod ridicol de simplu de a construi astfel de pătrate. Aceasta ar trebui să ia doar un pătrat, împărțiți-l în 16 celule, și fiecare dintre ele pentru a scrie numerele 1 la 16, iar apoi schimba numărul situat pe principalele diagonalele simetric față de centru, și o magie simetrică pătrat gata. Dürer rearanjate din sale pătrate de mijloc două coloane (care nu afectează proprietățile pătrat), astfel încât numerele din cele două celule de mijloc de linia de jos din oțel indică data creării tipărituri.
Cele mai vechi piețe de patru ori existente a fost găsit într-o inscripție XI sau XII secol, găsit în Khajuraho (India). El este prezentat în Fig. 143 în partea de sus.
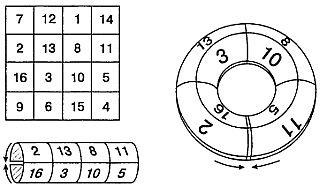
Acest pătrat magie se referă la varietatea de așa-numitele pătrate „diavol“ (sau „pandiagonalnyh“ sau „Nasiq“ chiar mai uimitor decât simetrică. În plus față de proprietățile obișnuite pătrate magice diabolice sunt toate „diagonalele polilinii“.
De exemplu, numărul de 2,12,15 și 5, precum și 2, 3,15 și 14 sunt pe diagonalele liniilor poligonale, care pot fi recuperate prin plasarea două pătrate adiacente identice. Piața Diavolului va fi diavolul în cazul în care este linia de sus în jos pentru a rearanja sau, dimpotrivă, linia de jos pentru a pune în sus, precum și în cazul în care să lovească ultima coloană la dreapta sau la stânga și să-l atribuie pătrat cu protipokazana în Fig. 144.
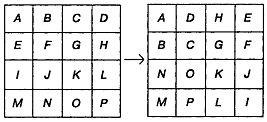
Fig. 144Odno transformări cinci proprietăți de conservare „diabolice“ „diavolului“ pătrat.
Combinând aceste cinci modificări, puteți obține 48 de tipuri de bază de pătrate diabolice (presupunând că o transformări valide includ rotații și reflecții, acest număr va crește la 384 tipuri). Așa cum arată și Rosser Walker, aceste transformări formează un „grup“ (adică o structură abstractă cu proprietăți definite), care coincide cu grupul transformă hipercub (cub cu patru dimensiuni) în sine.
Legătura dintre diavol și pătratele Hipercub nu este greu de văzut. dacă 16 celule pătrate, comparativ cu 16 vârfuri ale hipercubului. Corespondența dintre celule și vârfurile pot fi ilustrate prin familiare proiecția bidimensională a unui hipercub (Fig. 145).
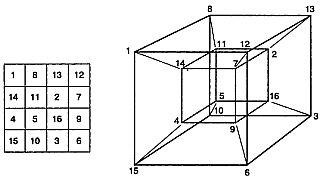
Fig. 145 hipercub „Diavolul“ și unul dintre ei 384 pătrate „diabolice“.
Suma numerelor la cele patru noduri ale fiecăreia dintre hipercubului 24 fețe pătrate este 34. perechi antipozi, rezultând un total de 17 sunt dispuse la capetele opuse ale diagonalelor hipercubului.
Răsuciți hipercub și producerea de reflecție, acesta poate fi tradus în 384 de poziții diferite, fiecare dintre care este afișat pe planul ca fiind una dintre cele 384 pătrate ale diavolului.
F. Claude Bragdon, celebrul arhitect american, care a murit în 1946, a constatat că prin combinarea celulelor una după alta patrate magice rupte linie, în cele mai multe cazuri, vom obține un model elegant. Modele similare pot fi produse prin combinarea celulelor cu numere numai chiar sau doar impare. Așa-obținut „linia magică“ Bragdon a fost folosit ca probe pentru desene de țesut, coperți de carte, decorative si decoratiuni arhitecturale headpieces. Ultima a făcut pentru fiecare capitol din autobiografia sa. Inventata le proiecta pentru grila de ventilație în plafonul Camerei de Comerț din Rbchestere (NY), unde a trăit, a fost construit dintr-un talisman magie rupt lo-shu. Un exemplu tipic de plan înclinat magic prezentat în Fig. 146, în cazul în care modelul este desenat direct pe pătrat Dürer.
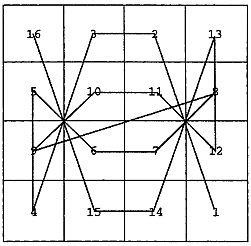
Fig. 146 „poligonal magic“ pentru pătrat Dürer.
[Este interesant faptul că teoria patrate magice de-a treia și de ordin superior este utilizat în mecanica cuantică moderne. În teoria cuantificarii momentului cinetic utilizat de așa-numita Regge tabel, care este un pătrat magic 3x3, compus din numere întregi arbitrare (nu neapărat numere întregi). Un astfel de tabel conține 5 numere întregi independente, respectiv, care au un element 3x3 pătrat 9, care sunt suprapuse pe cele 5 condiții cantități egale ale tuturor elementelor de rânduri și coloane unele întreg J. Tabelul Regge are forma:
Ha 6 numere pozitive j și m suprapusă starea j 1 + J 2 + 3 = J J; m 1 + m 2 + m 3 = 0 și condiția pentru pozitivitatea tuturor celor trei numere din primul rând. Aceste condiții sunt geometrically înseamnă că din cele trei segmente de lungime j 1. J 2. J3 poate forma un triunghi, astfel încât acestea sunt denumite colectiv „condiția triunghi.“ Substituind în tabelul orice valoare j pozitivă și m. îndeplinesc condițiile scrise, pentru a obține un pătrat cu magie suma J. Desigur, această metodă poate fi ușor generalizată la patrate magice cu elemente de fracționare și negative.
În cazul în care, în plus față de condițiile de mai sus și de a pune
apoi pătrat magică și suma membrilor cu care se confruntă fiecare diagonală este egală cu J.]
Capitolul 28. FIRM "HUGH JAMES RILEY, ATRACTII SI PUZZLE"
Printre cele mai mari companii din SUA sunt angajate în construcția de diverse divertisment, distracție și spectacol, fără îndoială, ar trebui să fie numit firma „James Hyu Rayli, atracții și puzzle-uri“, deși în realitate nu există ....
Auzind că la marginea nou deschis bâlci, carusel, și așa mai departe. N. Am decis să conduc acolo sus pentru a vedea vechiul său prieten Dzhimom Rayli. L-am întâlnit în anii '40, în timpul șederii studenților de la Universitatea din Chicago. În timp ce Riley a fost pe ultimul an de liceu, Facultatea de Matematica, atunci când dintr-o dată, cu totul neașteptat, el sa alăturat trupei itinerant pentru a deveni un artist de spectacol în Revue de dans. În acest rol după cum spun actorii, el a vorbit în următorii ani. În compania l-au numit profesor.
Într-un fel a reușit să păstreze un interes deosebit în matematică, iar atunci când nu ne-am întâlnit, am fost întotdeauna în măsură să extragă din ea unor teme originale pentru divertisment secțiune de matematică în Scientific American.
De data aceasta am găsit profesorii de la intrarea în spectacol ciudat, unde a discutat cu controlerul, verifica biletele. Era pălărie stetsonovskaya, iar el sa uitat mai în vârstă și mai solidă decât la ultima noastră întâlnire.
- Am citit în mod regulat profilul tau intr-o revista - a spus el cum ne-am dat mâna. - De ce nu scrie ceva despre cum să joace „Taci la fața locului“?
- Și ce este acest joc? - l-am întrebat.
- Aceasta este una dintre cele mai vechi atracții noastre.
Ma apucat de braț și târât pentru ei înșiși pe drumul cel bun. Curând ne-am oprit la o tablă pe care era pictat un cerc roșu cu un diametru de un metru. Profesorul mi-a explicat regulile. Jucătorul trebuie să plaseze cinci discuri metalice (de fiecare dată când luăm în considerare doar un singur disc), astfel încât au închis la fața locului roșu. Diametrul fiecărui disc a fost de aproximativ 61 cm. Punerea disc player nu are dreptul de a muta. Jocul este pierdut în cazul în care, după ce a pus ultimul, al cincilea disc va rămâne chiar și cea mai mică diferența și puteți vedea o pată roșie între discuri metalice.
- Desigur, - a spus profesorul - din toate cercurile pe care le puteți închide complet discul de diametrul cercului, am ales cea mai mare rază. Cei mai mulți oameni cred că discurile ar trebui să fie poziționate astfel încât. - Și el a pus conduce simetric.
Cu acest aranjament (vezi Fig. 147) de fiecare margine a discului trece prin centrul roșu al cercului (în desenul nostru este umbrită), iar centrul discului formează vârfurile unui pentagon regulat. Dar cinci bucăți mici de roșu la însăși marginea cercului rămâne neacoperit.