Funcția Intervalymonotonnosti. Puncte extremelor.
condiție monotonie. În cazul în care o funcție diferențiabilă mărește intervalul, atunci. În cazul în care o funcție diferențiabilă scade în intervalul, atunci.
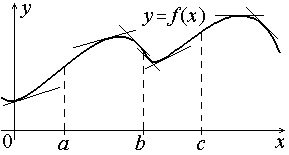
Punctul este un punct de minim al funcției, în cazul în care există o astfel încât pentru toți, în intervalul, și inegalitate.
Punctul se numește funcția maximă, în cazul în care există astfel încât pentru toți, în intervalul, și inegalitate.
puncte minime și maxime sunt numite puncte de funcții extreme.
Punct critic este un punct în care derivatul este zero sau nu există.
condiții suficiente pentru un extremum.
1. Dacă trece printr-un punct critic primelor modificări derivate semna, iar funcția este continuă la un punct, funcția de punct are o extremă. Mai mult decât atât, în cazul în care modificările semn de la „+“ la „-“, apoi - punctul maxim; în cazul în care semnul este schimbat de la „-“ la „+“, apoi - punctul de minim.
2. În cazul în care un punct critic al doilea derivat nu este zero și este continuă în punctul, funcția are un punct de extremum. Mai mult decât atât, în cazul în care punctul de al doilea derivat este pozitiv, atunci - un punct minim; în cazul în care, la punctul al doilea derivat este negativ, - punctul maxim.
Intervalyvognutosti și convexitate a funcțiilor graficului.
funcția convex Graph este chemat dacă tangent curbei în orice punct situată deasupra acestei curbe (Figura 9).
Graficul unei funcții este concavă pe în cazul în care tangenta
curbei în orice moment este sub această curbă (Figura 9).
condiție suficientă pentru convexitate. În cazul în care funcția este de două ori derivabila pe și pentru toate, graficul este convexă pe.
condiție suficientă de concavitate. În cazul în care funcția este de două ori derivabila pe și pentru toate, graficul este concavă pe.
Momentul în care se schimbă la concavitatea graficul unei cucui sau protuberanță pe contrabætætor numit un punct de inflexiune.
Punctul de inflexiune este o funcție de punctul în care funcția este continuă și
derivata a doua este egal cu zero sau nu există;
atunci când trece prin punctul de semn al doilea derivat.
Funcția de două variabile
O funcție de două variabile și set, în cazul în care fiecare pereche de numere și dintr-o anumită regiune pentru o anumită lege i se atribuie o valoare. Variabilele și sunt independente și - variabila dependentă (funcția).
Domeniul funcției este setul de puncte la care este definită funcția.
Numărul A se numește funcția limită a unui punct în cazul în care pentru orice există o astfel încât în cazul în care distanța dintre două puncte sau mai puțin, atunci:
Derivata funcției găsită în ipoteza că rămâne constantă se numește derivata parțială și este notat prin:
Derivata funcției găsită în ipoteza că rămâne constantă se numește derivata parțială și este notat prin:
Parțial funcția de ordinul 2 sunt numite derivații săi parțiale ale derivatelor parțiale de ordinul întâi:
- un al doilea derivat parțial;
- un al doilea derivat parțial;
- al doilea derivat amestecat parțial;
- al doilea derivat parțial amestecat.
Mixte derivate partiale egale între ele, cu condiția ca acestea să fie continuu :.
Diferențele de o funcție de două variabile:
- diferențial parțială a funcției;
- diferențial parțială a funcției;
- funcție totală diferențială.
Să o funcție de două variabile definite în mod implicit. . Dacă există sunt derivați continue, iar funcția implicită are derivate parțiale definite prin formulele:
plan tangent la suprafață, la un punct (punct de tangență) este un plan care conține toate tangentele la curbă trasată prin punctul de pe suprafață.
Normal la suprafață în punctul se numește o linie perpendiculară pe planul tangent la punctul și care trece prin punctul de tangență.
În cazul în care suprafața este dată în mod explicit, atunci ecuația de planul tangent la punctul este de forma:
și ecuația normală:
În cazul în care suprafața este dată implicit, ecuația planului tangent la punctul este de forma:
și ecuația normală:
Extremele funcțiilor de două variabile.
Un punct se numește punctul de minim al funcției, în care atunci când o anumită vecinătate a punctului pentru toate inegalitatea.
Un punct este numit un punct maxim al funcției, în care atunci când o anumită vecinătate a punctului pentru toată inegalitatea.
puncte minime și maxime sunt numite puncte de funcții extreme.
O condiție necesară pentru un extremum. Dacă funcția diferențiabilă are o extremă la punctul că derivații săi parțiale în ceea ce privește și în acest moment sunt egale cu zero:
Punctele în care derivatele parțiale ale funcției și sunt zero, numite staționare.
Punct critic este un punct în care derivatele parțiale cu respect și egală cu zero sau cel puțin una dintre ele nu există.
condiția suficientă a extremelor. Să - punctul critic. Notăm valorile derivatelor doilea, și. atunci
1) în cazul în care - punctul extremum al funcției, și - la punctul maxim și - la un punct minim;
2) Dacă, atunci nu există nici un extremum;
3) În cazul în care, atunci este necesară investigații suplimentare.
Metodele de bază de integrare.
I. Integrarea directă constă în reducerea integrală a unuia sau mai multor integralele tabulare utilizând proprietăți ale indefinită integrală și folosind diferite formule (inclusiv trigonometric) și identice transformări algebrice integrantul.
II. Metoda de a asocia un semn al diferențial este de a găsi sau de a crea o funcție în integrandul, astfel încât toate integrandul este înregistrată printr-o funcție specială:
III. Metoda de înlocuire variabilă este următoarea ecuație:
IV. Lăsați funcțiile și continuă împreună cu derivații săi, atunci avem formula de integrare prin părți:
Formula de integrare prin părți se aplică funcții continue, dar vă permite să calcula eficient nedefinită integrală numai pentru clase speciale de funcții:
1. În cazul în care integrala este de forma:
, în cazul în care - polinom de gradul
atunci cum trebuie să luați, și, ca să ia restul factorilor de integrandul, și anume
2. În cazul în care integrala este de forma:
, în cazul în care - polinom de gradul
atunci noi, si orice altceva pentru care este
3. Dacă integralei este de forma: sau formula de integrare prin părți, în acest caz aplicat de două ori, apoi integral inițial se exprimă algebric. Această integrare ciclică.
V. Integrarea fracțiilor raționale.
Expresia formei și în care - două grade și polinomială, respectiv (și - numere naturale) este o fracție rațională. În acest caz, în cazul în care fracția se numește propriu-zis. în caz contrar, în cazul în care - fracția se numește necorespunzătoare.
fracții Pur și simplu dreapta-raționale:
1) - elementar drobyuIvida;
3) - elementar drobIIIvida (- nu are rădăcini reale, adică);
4) - elementar drobIVvida (- nu are rădăcini reale;).
Fiecare fracțiune adecvată reprezentat ca o sumă a unui număr finit de fracții parțiale. În acest caz, în cazul în care numitorul luat:
în cazul în care - numerele naturale și apoi
Integrarea fracțiilor raționale de conducere:
Dacă fracțiune necorespunzătoare, este necesar să se prezinte ca o cantitate polinom și o fracțiune corespunzătoare;
Extinderea numitorul unei fracții raționale corect factoring și reprezintă ea ca sumă a celor mai simple fracțiilor raționale;
Integra polinom și suma rezultată din fracții parțiale.
VI. Integrarea funcțiilor iraționale.
1. Calculul integralelor de forma:
în cazul în care - o funcție rațională - întreg - număr real constant.
Aceasta este calculată integral prin substituirea
2. Calculul integralelor de forma:
în cazul în care - numerele naturale.
Integrala este calculată prin substituirea
unde - numitorul comun al fracțiunilor. Integrala va fi mai ușor în cazul în care - cel mai mic numitor comun al acestor fracțiuni.
VII. Integrarea anumitor expresii care conțin funcții trigonometrice.
1. În cazul în care integrandul poate fi scris ca produs al chiar puteri de sinus și cosinus, iar indicatorul cel puțin unul este negativ, după conversie poate fi obținută în conformitate cu funcția integrală sau dependente, și apoi să integreze, având în vedere că
Această substituție este utilizat, în cazul în care integrandul este o funcție rațională, în același timp,
În cazul în care modificările integrandul semnează numai atunci când se schimbă la, adică =, apoi se aplică substituția. În acest caz,
În cazul în care modificările integrandul semnează numai atunci când se schimbă la, adică =, apoi se aplică substituția. În acest caz,
5.Vychislenie integralelor
Unele cazuri speciale:
a) Să sinus și cosinus acelorași argumente, în acest caz, și - întregi ne-negative, și cel puțin una dintre ele este impar.
Dacă - un număr impar, atunci integrala este convenabil calculată prin substituție. Acesta utilizează identitatea pentru transformarea integrantul.
Dacă - un număr impar, atunci integrala poate fi calculată folosind substituție. În același timp.
b) În cazul în care - chiar și numărul de non-negativ, atunci calculul integralei este convenabil de a transforma integrantul folosind formule „grad de reducere“ și sinusul unghiului dublu:
6.Vychislenie integralele produse de funcții trigonometrice:
La calcularea integralelor acestei forme este convenabil pentru a înlocui funcțiile produsului în sumă, folosind ecuația:
7.Universalnaya substituție trigonometric:
Cu această substituire obținem
Pe intervalul este definită o funcție continuă. Lungimea punctelor arbitrare este împărțit în segmente parțiale, ..., și - cel mai mare dintre lungimile acestor segmente: unde. Punctul - puncte arbitrare ale segmentelor. Apoi, în cazul în care suma cumulată are o limită și care nu depinde de metoda segmentului de partiție sau prin selectarea punctelor (), această limită se numește integrala definită a funcției pe intervalul:
Proprietățile de bază ale integrala definită:
Metode de calcul a definit integral.