

Ecuația generală II curbei ordine.
Dacă ecuațiile curbelor: elipsei, hiperbola și parabole, cu axele de simetrie paralele cu axele dezvăluie paranteze, toate acestea pot fi reduse până la cinci atomi ecuație de ordinul 2, care are forma:
Este numit de ecuația generală a curbei de ordinul 2.
Analizând diferența de la fiecare alte ecuații de forma (1) pentru o elipsă, hiperbolă și parabole, se poate observa că, în cazul unei elipse - semne Coeficienți AiCodinakovy în cazul hiperbola - semnele koeffitsientovAiCrazlichny, iar în cazul parabolei unul dintre pătrate offline, care presupune egalitate zero, koeffitsientaAiliC corespunzătoare (odnovremennoAiCnulyu nu poate fi egal, în caz contrar ecuația obținută de ordinul 1, adică ecuația directă).
Astfel, curba ACopredelyaet produs a cărui ecuație este de forma (1).
Elipsă AC> 0;
Pentru hiperbola AC<0;
Pentru AC parabole = 0;
Să luăm în considerare problema inversă.
In sistemul de coordonate cartezian dat de ecuația:
Pentru a stabili curba și o imagine completă a modului în care este poziționat într-un plan, este necesar să se aducă ecuația (1) la o formă canonică, adică identifică pătrate perfecte în această ecuație.
De exemplu, vom da ecuația la forma canonică.
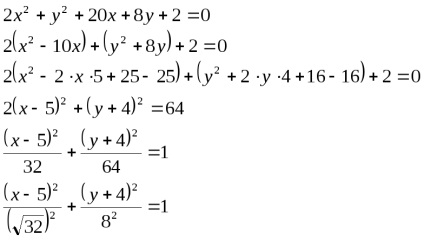
In sistemul de coordonate carteziene, ecuația de ordinul 2:
, Se poate satisface următoarele șapte tipuri de linii de ordinul al doilea. elipsă, hiperbolă, parabolică, o pereche de linii intersectate, puncte, o pereche de linii paralele, o pereche de linii de potrivire.
Care este locul geometric al punctelor definite prin ecuația
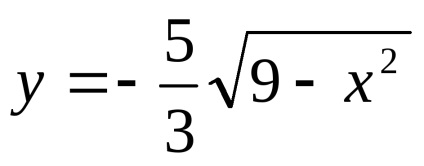
Având în vedere că partea dreaptă a ecuației nu este pozitiv, atunci
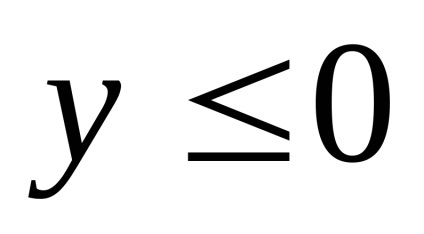
- este setul de puncte de elipsă ale cărei
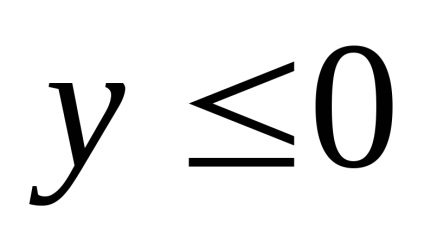


Conform acestei ecuații, se determină tipul curbei. Dă o ecuație de forma canonică, trage o curbă pe xOy plan. Găsiți coordonatele focii. Asigurați-ecuația de asymptotes pentru hiperbola:
A se vedea. Tabelul (1). Având în vedere ecuația curbei hiperbolic.
Aici este ecuația la forma canonică.
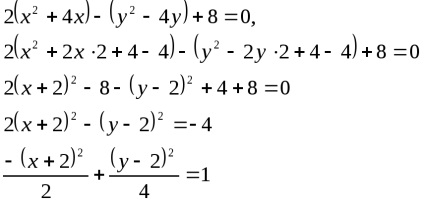
- ecuația canonică a hiperbola.
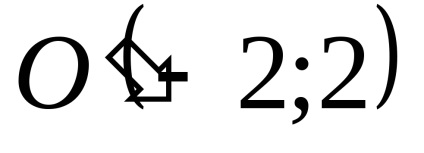

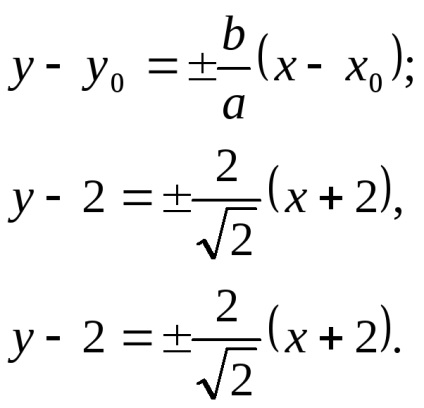
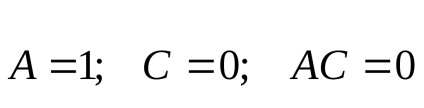
Având în vedere ecuația unei curbe de tip parabolic.
Aici este ecuația la forma canonică.
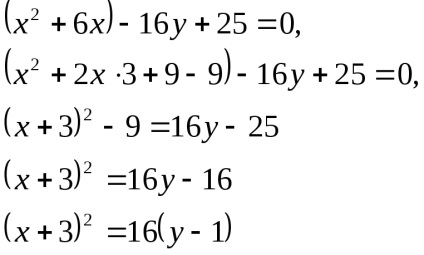
- ecuația canonică a unei parabole.
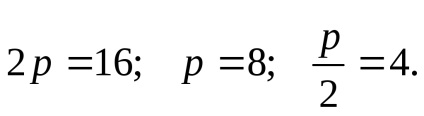
x = 0, atunci
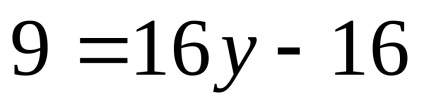
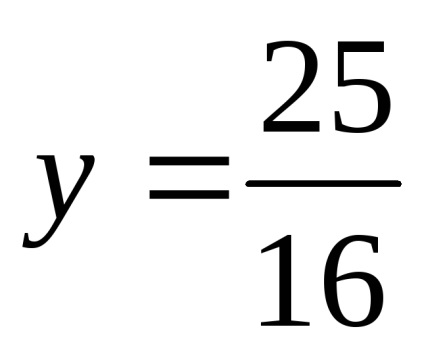
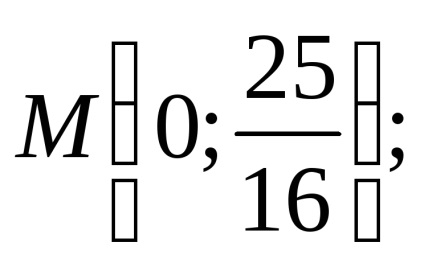


Având în vedere ecuația de tip hiperbolic. Noi da la o formă canonică.
Acesta este un caz de degenerare în liniile de intersectare hiperbola 2:
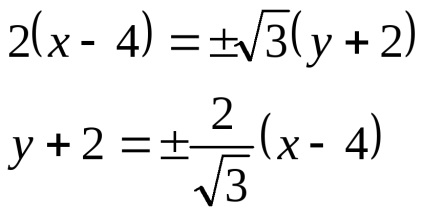
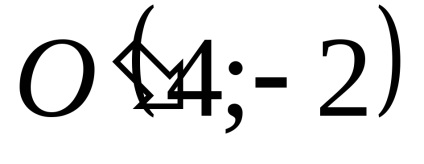
Pantele liniilor drepte:
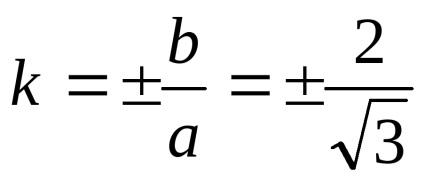
Avem aceste linii:
Având în vedere ecuația de tip curba eliptica.
Pentru a forma canonică.
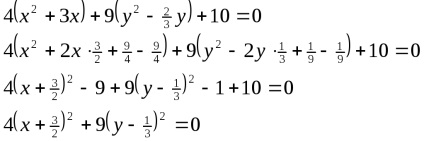
Acesta este un caz la punctul de degenerare elipsei
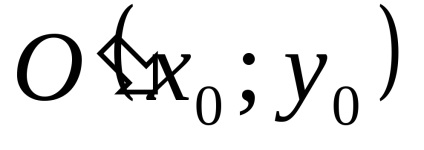
Acest lucru mulțumit de coordonatele de un singur punct:
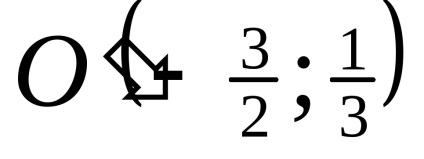
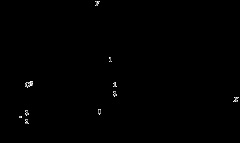

Construi o curbă definită de ecuația
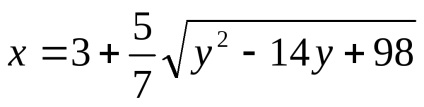
Această ecuație este echivalentă cu sistemul: sau, în consecință, în starea sa dat ecuația porțiunii hiperbolă
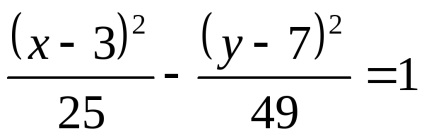
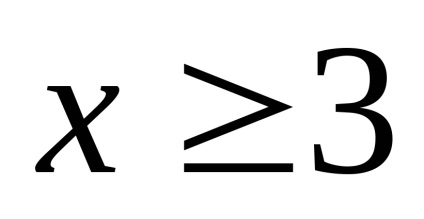
Noi construim doar ramura dreapta a hiperbola, ca este situat în semiplanul în cazul în care
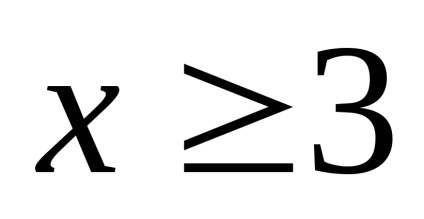


Construi o curbă definită de ecuația
Această ecuație este o porțiune curbă și este echivalentă cu următorul sistem:
În consecință, în condiția dată de ecuația porțiunii elipsei
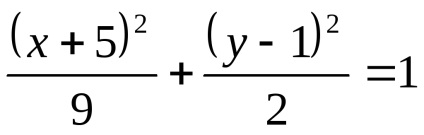
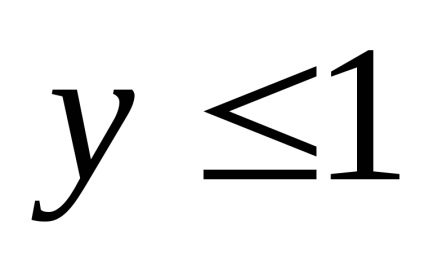


S. V. Frolov, R. Ya. Shostak, "Curs de Matematica Superioară", Moscova editura "High School", 1966.