Amintiți-vă cum în prima lecție, am vorbit despre zecimalele că există fracțiuni numerice, nu pot fi reprezentate ca zecimal (a se vedea. Lecția „fracții zecimale“)? Am învățat să se stabilească în numitorii asupra factorilor pentru a vedea dacă există, altele decât 2 și 5 numere.
Așa că am mințit. Și astăzi vom învăța cum să traducă numerice absolut orice fracție cu o zecimală. În același timp, familiarizat cu întreaga clasă fracțiuni cu o parte semnificativă infinită.
Repetarea zecimal - este orice zecimală, care:
- Semnificativ parte constă dintr-un număr infinit de cifre;
- La anumite intervale de numere în parte semnificativă repetate.
Un set de cifre repetate, care constituie o parte semnificativă, numită partea periodică a fracțiunii, precum și numărul de cifre în acest set - perioada fracțiunii. Restul părții semnificative segment pe care nu se repetă se numește o parte non-periodice.
Deoarece multe definiții, este necesar să se ia în considerare în detaliu câteva dintre aceste fracțiuni:
Această fracțiune se găsește în probleme mai des. parte neperiodice: 0; parțial periodică 3; Durata perioadei: 1.
parte neperiodice: 0,58; parțial periodică 3; Durata perioadei: 1 din nou.
parte Nonperiodic 1; parte periodică 54; Durata perioadei: 2.
parte neperiodice: 0; parte periodică: 641025; Durata perioadei: 6. Pentru comoditate, repetând părți separate printr-un spațiu - în decizia de a face acest lucru nu este necesar.
parte neperiodice: 3066; parțial periodică 6; Durata perioadei: 1.
După cum puteți vedea, determinarea periodică a fracțiunii bazată pe conceptul significand. Prin urmare, dacă ați uitat ce este recomandabil să se repete - vezi lecția „înmulțirea și împărțirea de zecimale.“.
Trecerea la zecimal periodice
Să considerăm o fracție comună a forma a / b. Expand-l numitorul în factori de prim. Există două opțiuni:
- În extinderea există doar 2 multiplicatori și 5. Aceste fracțiuni sunt ușor de zecimale - a se vedea lecția „fracții zecimale.“. Acestea nu ne privesc;
- În expansiunea există altceva în afară de 2 ceva și 5. În acest caz, fracțiunea nu poate fi reprezentat ca o zecimal, dar de la ea putem face o zecimală repetitivă.
Pentru a seta zecimal repetitivă, trebuie să găsim o parte sa periodice și aperiodice. Cum? Puneți rola în greșit, și apoi împărțiți numărătorul de numitor „zona.“
Aceasta va avea loc după cum urmează:
- În primul rând împărțit întreaga parte. în cazul în care există;
- Acesta poate fi de mai multe numere de după virgulă;
- După un timp, numerele încep să se repete.
Asta este! Numerele repetate după virgulă denotă partea periodică, dar ceea ce stă în față - un non-periodice.
Sarcină. Rândul său, fracții ordinare în zecimale periodice:
Toate fracțiile fără întreaga parte, astfel încât diviza doar numărătorul de numitor „colț“:
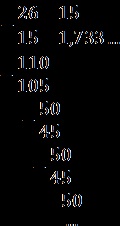
După cum puteți vedea, resturile sunt repetate. Scriem fracțiunea de pe „dreapta“ modul în care: 1733. = 1,7 (3).
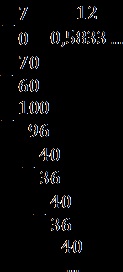
Rezultatul este o fracție: 0.5833. = 0,58 (3).
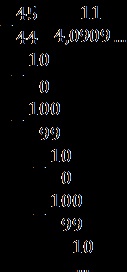
Scrie într-un mod normal: 4.0909. = 4 (09).
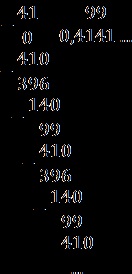
Ne-am împușcat: 0.4141. = 0, (41).
Tranziția de la fracție zecimală periodică la un obișnuit
Luați în considerare repetarea zecimală X = abc (a 1 b 1 c 1). Necesar să-l traducă într-un clasic „cu două etaje“. Pentru a face acest lucru, efectuați patru pași simpli:
- Găsiți o perioadă de fracție, adică Numărați câte numere sunt în partea periodice. Să fie numărul de k;
- Găsiți valoarea expresiei X · 10 k. Acest lucru este echivalent cu trecerea punctului zecimal spre dreapta pentru o perioadă completă - vezi lecția „Înmulțirea și împărțirea de zecimale“ ;.
- Din acest număr trebuie să deducă expresia inițială. Atunci când această parte periodică a „remanentă“, și este, în general concasat;
- În ecuația rezultată a X. găsi toate zecimalele traduce în acțiuni ordinare.
Sarcină. Se aduce la comune fracții improprii de:
Lucrăm cu prima fracție: X = 9, (6) = 9.666.
doar un singur număr este cuprins între paranteze, astfel încât perioada de k = 1. Apoi înmulțim această fracție cu 10 k = 10 ianuarie = 10. Avem:
10 · 10 X = 9.6666. = 96.666.
Scădeți împușcat inițială și de a rezolva ecuația:
10 X - X = 96666. - 9.666. = 96-9 = 87;
9 X = 87;
X = 87/9 = 29/3.
Acum vom înțelege a doua fracție. Astfel, X = 32 (39) = 32.393939.
Perioada k = 2, astfel încât multiplica toate cele 10 k = 10 2 = 100:
X = 100 · 100 32.393939. = 3239.3939.
Din nou, scădem împușcat inițială și de a rezolva ecuația:
100 X - X = 3239,3939. - 32.3939. = 3239-32 = 3207;
99 X = 3207;
X = 3207/99 = 1069-1033.
Pornirea treia fracțiune: X = 0,30 (5) = 0.30555. Schema este același, așa că voi da doar calculele:
Perioada k = 1 ⇒ multiplice toate 10 k 10 = 1 = 10;
10 · 10 X = 0.30555. = 3.05555.
10 X - X = 3,0555. - 0.305555. = 2.75 = 4.11;
9 X = 11/4;
X = (11/4). 9 = 11/36.
În cele din urmă, ultima fracțiune: X = 0, (2475) = 0.2475 2475. Din nou, pentru comoditate părți periodice sunt separate unele de altele prin spații. Avem:
k = 4 ⇒ 10 k = 10 4 = 10,000;
X 10,000 = 10,000 2475 · 0.2475 = 2475.2475.
10 000 X - X = 2475,2475. - 0,2475 = 2475. 2475;
X = 2,475-9,999;
X = 2475. 9999 = 25/101.
- compararea fracțiunilor
- Testul pentru lecția „fracții zecimale“ (opțiunea 2)
- Combinatorică în B6 problema: testare ușor
- Care este fracțiunea numerică
- ecuație plan în C2 sarcină. Partea 1: matrice și factorii determinanți
- Webinar privind sarcinile C1: Trigonometrie
- Pregătirea gratuită pentru examenul de 7 lecții simple, dar foarte util + teme pentru acasă
