În acest termen, există alte utilizări, a se vedea. Prism.
Prism - un element optic realizat din material transparent (de exemplu, sticlă optică), sub forma unui corp geometric - prismă. având o suprafață plană lustruită prin care lumina intră și iese. Lumina este refractata într-o prismă. Cea mai importantă caracteristică a prismei este indicele de refracție al materialului din care este făcută.
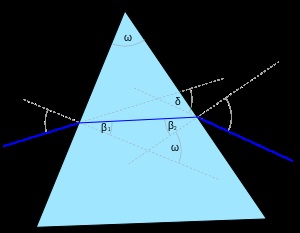
Calea de raze într-o prismă triunghiulară
Calea de raze într-o prismă triunghiulară
Cel mai simplu tip Prisma este o prismă triunghiulară, adică un corp, care este o formă geometrică cu două baze prisme triunghiulare și trei fețe laterale în formă de dreptunghiuri.
Figura prezintă o secțiune a unui plan paralel cu prisme triunghiulare, bazele sale. Legendă: δ - deformarea unghiului, ω - unghiul de refractie [1] prismei, alfa 1. β 2, \ beta _> - unghiuri de incidență, respectiv, care intră prin partea laterală a prismei fasciculului și fasciculul ieșind prin cealaltă parte a feței, p 1 . 2 alfa, \ alpha _> - unghiuri de refracție ale celor două grinzi, respectiv. În această figură, materialul prismă - un mediu optic mai dens decât împrejurimile sale, deoarece unghiul de incidență a razei de intrare este mai mare decât unghiul de refracție. Aceasta este, indicele de refracție relativ al materialului - este mai mare decât unu, notat cu n. Cea mai simplă formulă pentru unghiul de deviere este obținut, presupunând că unghiul prismă de refracție și unghiul de incidență a razei de intrare este mică [2]. Apoi, va fi mic și unghiul α 2>. și, prin urmare, va fi mică, iar unghiurile p 1. β 2, \ beta _>. Conform legii de refracție a luminii:
α 1 ≈ păcatul a 1 = n ⋅ păcat p 1 ≈ n ⋅ β 1. \ approx \ păcatul \ alpha _ = n \ cdot \ păcatul \ beta _ \ aprox n \ cdot \ beta _,> α 2 ≈ păcatul α 2 = n ⋅ păcat p2 ≈ n ⋅ β 2 \ approx \ păcatul \ alpha _ = n \ cdot \ păcatul \ beta _ \ approx n \ cdot \ beta _>
π - δ + π - ω + α 1 + α 2 = 2 π. + \ Alpha _ = 2 \ pi> δ = α 1 + α 2 - ω ≈ n ⋅ (β 1 + β 2) - ω = n ⋅ ω - ω = (n - 1) ⋅ ω + \ alpha _- \ omega \ approx n \ cdot (\ beta _ + \ beta _) - \ omega = n \ cdot \ omega - \ omega = (n-1) \ cdot \ omega>
Astfel, la un unghi mic de incidență a razei de intrare avem o formulă aproximativă pentru unghiul de deviație:
Această formulă este mai important, deoarece aceasta poate ajuta pentru a deduce dependența distanței focale a unei raze de lentilă subțire de pe suprafața acestuia, în care obiectivul este înlocuit cu o prismă triunghiulară subțire se folosește și formula pentru unghiul de deflexie [3].
În cazul unghiului arbitrar prismă de refracție și unghiul de incidență a razei de intrare, iar în cazul în care indicele de refracție absolut al materialului prismei este egal cu n 2>. și împrejurimi - n 1>. Considerații similare se pot obține o formula [4]:
prismă de dispersie

prismă Dispersive utilizate în instrumente spectrale pentru separarea spațială a diferitelor lungimi de undă de emisie.
- Un simplu prismă cu trei tăișuri
- Browning Prism-Rutherford
- prismă Dispersive Abbe
- Amici prisme (vizualizare prism directă)
- prismă Littrow
- prismă Cornu
- Pellin-Broca prismă
prismă reflectorizant
Prisma reflectorizant este folosit pentru a schimba calea razelor, schimbând direcția axei optice, de vedere schimbări de direcție linie, în scopul de a reduce dimensiunea totală dispozitiv. Clasificate prisme reflectorizante pe mai multe caracteristici:
- numărul de reflecții din prisma
- prezența sau absența unui „acoperiș“
- Structura prismă de caractere
- îndoiți colț de axa optică
De asemenea, o nișă specială printre prisme reflectorizante ocupă prisme compozit - format din mai multe părți, separate prin golurile de aer. Unele prisme răspândite au fost numite.
numele prismă desemnat de două sau trei litere și numărul de cratimă înregistrate. Prima literă reprezintă numărul de fațete reflectorizante (reflecții) în prisma. ( "A" - un "B" - două "B" - trei, etc ...). „Acoperiș“, în mod convențional, este o fațetă a desemnării sale și de a pune indicele „k“, după prima literă. (De exemplu, Ak, Bk) rămase litere indică caracterul structurii. ( "P" - isoscel, "P" - pentaprismei, "Y" - polupentaprizma, "C" - ortorombic, "M" - tip variind de "A" - prismă Lehmann). Cifrele înregistrate cratimă indică unghiul cârcel al axei optice. (0 °, 90 °, 180 °). De exemplu, „CMR-45 °» - Prisma isoscel cu trei laturi reflectorizante și un acoperiș, cu o îndoitură axa 45 °.
prisme compuse sunt indicate prin numele lor proprii și colțuri axa fractură. De exemplu, „A-0 °» - Abbe prismă, „Bk-90 °» - prism pantof cu un acoperiș, „K-0 °» prismă --cube.