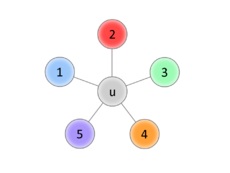
și în legătură cu ea de sus
Început de Demonstrația este aceeași ca și în teorema anterioară, dificultatea apare în pasajul de inducție. Arătăm că pentru cazul în culori th vă puteți întoarce în continuare în partea de sus a telecomenzii, astfel încât colorația a rămas corectă.
Notăm pentru - se întoarce în top - top, vopsite în culoare.
Dacă printre nodurile adiacente, există două vârfuri de aceeași culoare, apoi rămâne cel puțin o culoare liberă, în care vom picta.
In caz contrar, a pus obținut după îndepărtarea unui grafic pe un plan, înapoi vertex (până incolor) și numărul de culori în ordinea parcurgeri nodurilor adiacente în sensul acelor de ceasornic.
Să încercăm să picteze în culori. Pentru a colorat a rămas corectă, vopsi culoarea nod adiacent. Dacă printre vârfurile adiacente sunt ele vopsea nod de culoare, și așa mai departe. Luați în considerare două situații neobișnuite care pot apărea în timpul unei crawl:
- vom ajunge să avem o dată revopsit partea de sus (și doriți să re-vopsea-l înapoi, care nu se poate face). Este evident că o astfel de situație este imposibilă, pentru că ne-am schimbat culoarea vârful schemei, iar dacă la sfârșit am primit un by-pass două noduri adiacente de aceeași culoare, și apoi să recolors în acest loc au existat două vârfuri de aceeași culoare, iar pe grafic ipoteza fara a fost pictat corect.
- vom ajunge la partea de sus, adiacent, care a avut inițial de culoare, care nu poate fi revopsit în modelele (are acum o culoare).
În cazul în care acest proces a fost finalizat cu succes, vei primi colorat regulat. Dacă în zugrăvirea nu a reușit în conformitate cu al doilea exemplu de realizare, aceasta înseamnă că graficul are un ciclu.
Apoi, încercați același mod revopsite în culori, și adiacente acesteia de culoare (cu revopsire ulterioare). Dacă vom reuși - Colorația obținut.
Dacă nu, atunci am primit un alt ciclu. Dar grafic planar, apoi a primit două cicluri se suprapun, în plus față de partea de sus a cel puțin una, ceea ce este imposibil, pentru că partea de sus a primului ciclu, iar al doilea - în culori diferite. Deci, acest caz nu poate avea loc.