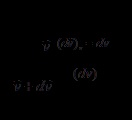
, și energia cinetică (*)
La sfârșitul particulelor în mișcare în activitatea v.1 v.2 este egal cu:
(**)
Ie incrementul energiei cinetice a particulei atunci când se deplasează de la Volum 1 la volumul 2 al câmpului de forță este egală cu suma algebrică a activității tuturor forțelor care acționează asupra particulei în această mișcare.
În cazul în care, apoi - cinetică crește energia. În cazul în care - este redusă (în acest fel acționează forța de rezistență).
Ecuațiile (*, **) valabile în cadre de referință inerțiale și neinertiale. În trecut, este necesar să se lucreze tot afară să se ia în considerare activitatea forțelor de inerție.
Toate subiectele acestei secțiuni:
mișcare mecanică.
Materia se știe că există în două forme: ca o chestiune și pas. Primul tip include atomii și moleculele din care sunt construite toate organismele. Al doilea tip include toate tipurile de câmpuri: gravitate
Spațiu și timp.
Toate corpurile există și pentru a muta în spațiu și timp. Aceste concepte sunt fundamentale pentru toate științele naturale. Orice organism are dimensiuni, adică, amploarea lor spațială
Sistemul de referință.
Pentru a identifica în mod unic poziția corpului în orice moment aveți nevoie pentru a selecta un sistem de referință - un sistem de coordonate, ore snabzhennuya și svyazannuya tare cu un corp solid complet, pentru
Ecuațiile cinematice ale mișcării.
Când conduceți tm coordonate și schimbare a lungul timpului său, astfel încât să definească legea de mișcare trebuie să specifice tipul de fe
, Deplasarea elementară în mișcare.
Să punctul M se mută de la A la B pe calea curbată AB. În momentul inițial al vectorului său este raza
Accelerarea. accelerația normală și tangențială.
mișcare punct se caracterizează printr-o schimbare a vitezei de accelerare viteză. În cazul în care viteza punctului de un timp arbitrar
mișcare de translație
Cea mai simplă formă de mișcare mecanică a corpului rigid este mișcare de translație în care linia dreaptă care unește două puncte ale unui corp se deplasează cu corpul, rămânând paralele | ei
sistem de referință inerțial.
Este cunoscut faptul că mișcarea mecanică relativă și natura sa depinde de alegerea sistemului de referință. Prima lege a lui Newton nu se realizează în toate cadrele de referință. De exemplu, corpul întins pe o n buna
Greutate. A doua lege a lui Newton.
Obiectivul principal este de a determina dinamica caracteristicilor mișcării corpurilor sub acțiunea forțelor aplicate acestora. Din experiență știm că sub forța
Legea fundamentală a dinamicii unui punct material.
Ecuația descrie variația mărimii mișcării finale a corpului sub efectul absenței deformare, și dacă
Legea a treia a lui Newton
Observațiile și experimente indică faptul că acțiunea mecanică a unui corp pe altul este întotdeauna interacțiune. În cazul în care corpul 2, acționează asupra corpului 1, corpul 1 este necesară pentru a contracara cele
transformarea galilean
Acestea vă permit să se determine cantitățile cinematice în tranziția de la un sistem de referință inerțial la altul. lua
principiul relativității lui Galileo
Accelerarea orice punct în toate cadrele de referință, mișcare unul față de altul în mod uniform, la fel:
cantitățile conservate
Orice organism sau mai multe organisme ale sistemului sunt un set de puncte sau particule de material. Starea sistemului la un moment dat în mecanica este determinată prin specificarea coordonatelor și vitezele în
Centrul de masă
În orice sistem de particule poate găsi un punct numit centrul de masă
Ecuația de mișcare a centrului de masă.
Legea fundamentală a dinamicii poate fi scrisă într-o altă formă, cunoscând conceptul centrului de masă al sistemului:
forțele conservatoare
Dacă la fiecare punct al particulei este plasată acolo, forța, spune că particula este într-un câmp de forță, de exemplu în domeniul gravitației, gravitațional, Coulomb și alte forțe. câmp
Forțele centrale.
Orice câmp de forță cauzată de acțiunea unui sistem de organism specific sau organisme. Forța care acționează asupra unei particule în domeniul
Energia potențială a unei particule într-un câmp de forță.
Faptul că forța conservatoare de muncă (pentru câmpul staționar), depinde numai de pozițiile de plecare și se termină cu o particulă în domeniu, permite introducerea conceptului fizic potential important
Comunicarea între potențialul de energie și forță pentru domeniul conservator.
Interacțiunea dintre particulele cu organismele din jur pot fi descrise în două moduri: folosind conceptul de forță sau prin intermediul unor potențiale concepte energetice. Prima metodă este mai general. deoarece este aplicabilă forțelor
Energia mecanică totală a particulei.
Este cunoscut faptul că creșterea energiei cinetice a particulei atunci când se deplasează într-un câmp de forță este o lucrare elementară a tuturor forțelor care acționează asupra particulei:
Legea conservării energiei mecanice a particulei.
Din expresie rezultă că în câmpul staționar al forțelor conservatoare, energia mecanică totală a particulei poate fi modificată
Cinematica.
Rotirii corpului poate fi la un unghi
Momentul de impuls al particulei. Momentul de forță.
În plus față de energia și impulsul, există o altă cantitate fizică, care este asociat cu legea de conservare - acest impuls. Momentul de impuls al particulei
un moment cinetic și momentul forței în jurul axei.
Ia un interes în noi un cadru de referință unei axe fixe arbitrare
Legea conservării momentului cinetic al sistemului.
Să considerăm un sistem format din două particule interacționează, care acționează ca forțe externe și
Ecuația corpului rigid dinamica de rotație.
Ecuația corpului rigid dinamica de rotație poate fi obținută prin scrierea ecuației pentru corpul rigid momentele de rotație în jurul unei axe arbitrare
Energia cinetică a unui corp de rotație.
Să considerăm un corp absolut rigid rotește în jurul unei axe fixe care trec prin. Împarte în particule cu volume mici și mase
Forța centrifugă de inerție
Să considerăm un disc care se rotește împreună cu mingea pe un arc plasat peste ac, Figura 5.3. Mingea este
forța Coriolis
Când corpul se deplasează în raport cu CO prin rotație în afară. mai există o forță, forța Coriolis și forța Coriolis
mici oscilații
Luați în considerare un sistem mecanic. Poziția poate fi determinată pomoschyu o valoare, de exemplu x. În acest caz, se spune că sistemul are un grad, acesta poate fi svobody.Velichinoy
oscilații armonice.
Ecuația 2 nd Legea Nyutona în absența forțelor de frecare pentru tipul de forță cvasi-elastică este după cum urmează:
pendulă
Acest punct de material suspendat pe o lungime fire neextensibil. pendulează în Pln vertical
pendul fizic.
Acest solid, oscilează în jurul unei axe fixe atașat la corp. Axa este perpendicular pe desen și pui de somn
oscilație amortizată
Într-un sistem real, există forță de rezistență de vibrație, a cărei acțiune conduce la o scădere a potențialului energetic al sistemului, și fluctuațiile în cel mai simplu caz va zatuhayuschimi.V
Auto-oscilații
În cazul în care energia de oscilație amortizată a sistemului scade treptat și oscilațiile opresc. Pentru a face neamortizate lor, este necesar să se alimenteze de energie din afara sistemului la un anumit punct
oscilații forțate
Dacă sistemul oscilant, în plus față de forțele de rezistență, este expus la o forță externă periodică, schimbarea armonică
rezonanță
Dependența de amplitudinea oscilațiilor forțate care rezultă din faptul că, la un anumit dată sistemului
Propagarea undelor într-un mediu elastic.
Dacă, în orice loc din mediul elastic (solid, lichid, gazos) pentru a plasa sursa de oscilații, datorită interacțiunii dintre particulele vor fi distribuite in oscilatie a particulelor medii la h
plan de ecuații și valuri sferice.
Ecuația Wave exprimă dependența deplasării particulei oscilante din kordinaty acesteia.
Ecuația undei
Ecuația Wave este soluția unei ecuații diferențiale, numită unda. Pentru a găsi stabilirea lui derivați ai doua parțiale în ceea ce privește timpul și coordonatele din ecuația