În ecuațiile (1) sau (2), cea mai mare cilindree a pendulului din poziția de echilibru a poziției numită amplitudine de deplasare (xmax). În sistemul SI al unității sale - metru:
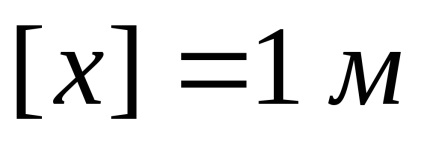
Expresia în paranteze de ecuații (1) sau (2) se numește faza de oscilație
Unitatea este faza de radian:
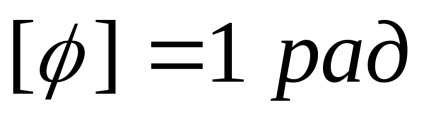
La momentul inițial (începutul mișcării) faze este
,
Prin urmare, valoarea 0 numită faza inițială. Acesta poate fi luată egală cu 0.
Cantitatea numită ciclică (sau unghiulară) frecvența vibrațiilor. Se măsoară în radiani pe secundă:
.
În cursul valorii sale nu se schimba oscilațiilor. magnitudine legate de magnitudine n Sa. numita frecvență de oscilație, formula:
În consecință, având în vedere cu formula (4), expresia (3) pentru faza și legea de oscilație (1) ia forma respectiv:
Prin definiție, oscilațiile relative chastotaravna chislaNpolnyh făcute pentru vremyat, de data aceasta:
Această valoare este măsurată în hertzi:
.
Sensul fizic al frecvenței este că acesta este numeric egal cu numărul de oscilații complete pe unitatea de timp, t. E. Pentru 1 s
.
Valoarea egală cu oscilațiile de timp în raport cu numărul de oscilații nazyvayutperiodomkolebany
Perioada se măsoară în secunde:
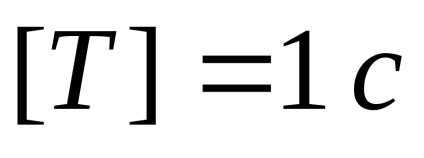
Sensul fizic al perioadei este că acesta este numeric egal cu timpul de o oscilație completă
.
Prin urmare, perioada asociată cu frecvența și frecvența ciclică a formulelor:
Astfel, având în vedere formulele (8), expresia (3) pentru faza și legea de oscilație (1) ia forma:
Energia mecanică de oscilații armonice
Energia oscilațiilor mecanice este egală cu suma dintre energia potențială și energia cinetică:
Energia este măsurată în jouli:
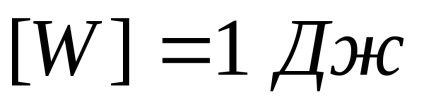
Energia potențială a masei pendulului este proporțională cu pătratul frecvenței de oscilație, pătrat coordonate (offset) este egal cu pendulul și
Substituind în ecuația (10) drept oscilație (1), atunci
Este evident că energia potențială variază periodic în timp. Perioada de pătrat a cosinusul de 2 ori mai mică decât perioada de cosinus, prin urmare, perioada de schimbare a potențialului energetic în mai puțin de 2 ori perioada coordonatelor schimbare. Pentru una oscilație completă a energiei potențiale pendulului devine de două ori zero când pendulul trece poziția de echilibru și de două ori are valoarea maximă la deplasarea maximă a pendulului.
Valoarea maximă a energiei potențiale este
Energia cinetică este proporțională cu masa pendulului și pătratul vitezei de vibrație:
Un raport de schimbare a vitezei egală cu coordonatele timpului acestei schimbări:
Unități de viteză - metru pe secundă:
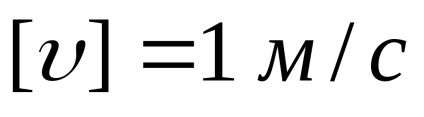
Substituind ecuația (1) în expresia (14), obținem:
.
Amplitudinea fluctuațiile de viteză este
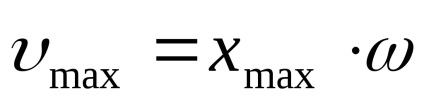
O expresie pentru viteza la pătrat vozvedom și înlocuind în ecuația (13):
În consecință, valoarea energiei cinetice, de asemenea, se schimbă periodic în timp, iar pentru o oscilație completă energie potențială devine zero, de două ori atunci când pendulul este mutat cât mai mult posibil, și de două ori are o valoare maximă în poziția de echilibru a pendulului.
Valoarea maximă a energiei cinetice este aceeași ca și potențialul, în cazul în care nu există nici o pierdere de energie.
Acum vom găsi energia mecanică totală a pendulului, înlocuind expresiile (11) și (15) în ecuația (9):
Astfel, pe parcursul perioadei de oscilație, energia mecanică totală a pendulului este constantă și egală cu amplitudinea energiei potențiale și cinetice.