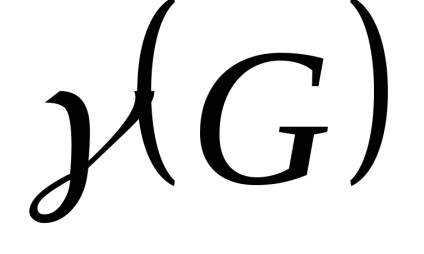1. Introducere
O varietate de probleme care apar în planificarea producției, pregătirea orarelor de inspecție, depozitarea și transportul de mărfuri, etc. Acesta poate fi adesea prezentată ca o problemă a teoriei grafurilor, care este strâns asociat cu așa-numitul „Colorând de locuri de muncă.“ Graficele discutate în acest capitol nu sunt orientate și nu au bucle; Dacă nu este stipulat în mod expres altfel, cuvântul „Graficul“ înseamnă exact acest grafic.
conte englez

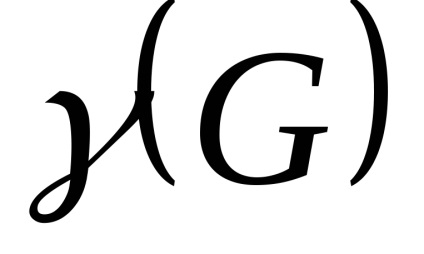
În general vorbind, numărul cromatic al unui grafic (precum și numărul de independență și dominație, discutat în capitolul anterior) nu poate fi găsit, știind doar numărul de noduri și muchii ale unui grafic. Nu este suficient să cunoască bine gradul de fiecare nod pentru a calcula numărul cromatic al unui grafic. Acest lucru poate fi văzut prin considerarea graficele prezentate în figura 1 (a) și Fig.1 (b). Aceste grafice sunt pentru n = 12 noduri, m = 16, coastele și aceeași distribuție a gradului de vârfuri
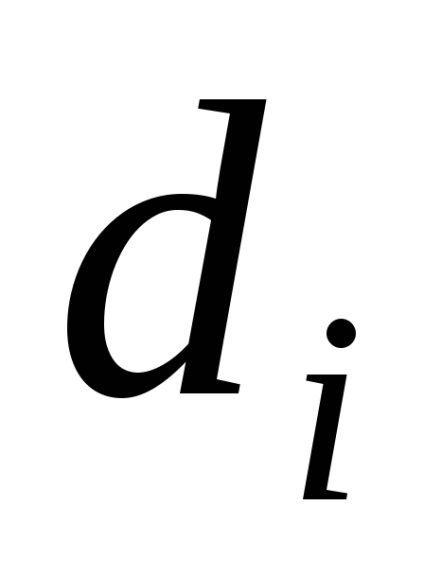

Problema de a găsi numărul cromatic al unui grafic arbitrar a făcut obiectul a numeroase studii și la sfârșitul secolului al XIX în secolul actual. Acum, pe acest subiect cunoscut la un număr mare de rezultate interesante. În acest capitol, cu toate acestea, noi nu încercăm să discutăm aceste rezultate, sau cel puțin să le dea o scurtă trecere în revistă. Introducem doar acele concepte care sunt necesare pentru a construi algoritmi pentru rezolvarea problemei a graficului de colorat. Aici considerăm algoritmii de bază (exactă, cât și „aproximativă“), permițându-ne să găsim (exactă sau aproximativă) valoarea numărului cromatic al unui grafic arbitrar și valoarea corespunzătoare a colorat nod.
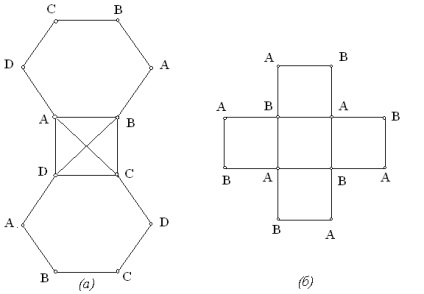
Fig.1. Două grafice cu același n, m și distribuția gradului de noduri, dar diferite numere cromatice. (A)
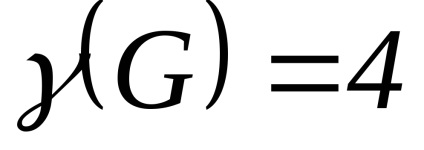
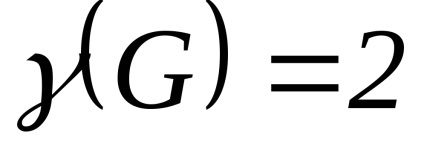
2. Unele teoreme și estimări referitoare la numărul cromatic
2.1. limite inferioare pentru.
Pe măsură ce numărul de
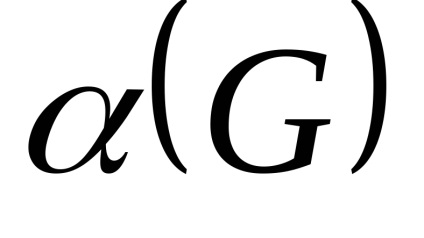
unde n - numărul de noduri și G.
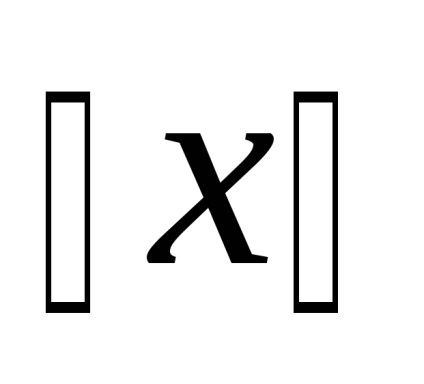
O altă estimare mai mici pentru