accelerație centripetă la mișcare uniformă circumferențial
Lăsați punctul materialul se mișcă uniform într-un cerc. Apoi, modulul nu se schimba viteza sa ($ v = const $). Dar acest lucru nu înseamnă că accelerația unui punct material este egal cu zero. Vectorul viteză tangențială la calea punctelor de mișcare. Atunci când se deplasează în jurul circumferinței viteza își schimbă direcția în mod constant. Deci, punctul este accelerat.
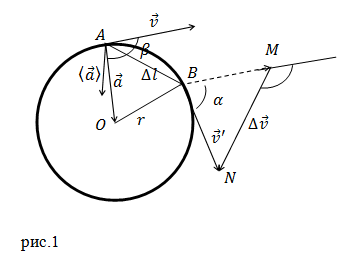
Luați în considerare punctele A și B aparținând la traiectoria corpului în mișcare. modificări vector de viteză pentru aceste puncte este egal cu:
Atunci când deplasarea între punctele A și B este mic, arcul AB este puțin diferită de coarda AB. BMN triunghi AOB și altele similare, prin urmare:
Modulul mediu accelerație este găsit ca:
Accelerația instantanee poate fi obținută prin a merge la limita ca $ \ Delta t \ la 0 \ $ de $ \ left \ Langle un \ drept \ rangle $:
Vectorul unghiului mediu de accelerație și vectorul viteză este egală cu:
Când $ \ Delta t \ la 0 \ unghi $ $ \ alpha \ la 0. $ dovedește că vectorul accelerație instantanee este un vector de viteză unghi $ \ frac $.
Am constatat că un punct material, se deplasează uniform într-un cerc, este accelerat spre centrul căii de deplasare (perpendicular pe vectorul de viteză), magnitudinea sa este egală cu viteza la pătrat împărțită la raza cercului. Această accelerare se numește centripetă sau normal. indică faptul că este de obicei _n $ $.
unde $ \ omega $ - viteza unghiulară a mișcării unui punct ($ v = \ omega \ cdot r $).
Definiția accelerare centripete
Și astfel, accelerația centripetă (în general) - o componentă a accelerației totală a punctului material, care caracterizează cât de repede se schimbă direcția vectorului de viteză în mișcarea curbilinie. O altă componentă a accelerației totale este accelerația tangențială, este responsabil pentru modificarea magnitudinea vitezei.
accelerația centripetă este:
unde $ e_r = \ frac> $ - unitate vector direcționat din centrul de curbură al traiectoriei la punctul respectiv.
S-au obținut formula corectă în primul rând pentru Huygens accelerare centripete.
Unitatea de măsură a accelerației centripete în Sistemul Internațional de unități este metru pătrat împărțit de a doua:
Exemple de probleme cu soluție
Sarcină. Discul se rotește în jurul unei axe fixe. Legea schimbă raza unghiului de rotație a discului dată de ecuația: $ \ varphi = 5t ^ 2 + 7 \ (rad) $. Care este accelerația centripetă Un punct de antrenare, care se află la o distanță de $ r = $ 0,5 m de axa de rotație până la sfârșitul celei de a patra secunde de la începutul rotație?
Decizie. Fă un desen.
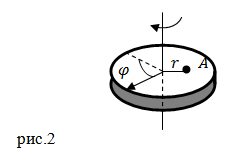
accelerare centripet Modulul este:
Punct de viteză unghiulară este găsit ca:
ecuația modifică unghiul de rotație, în funcție de timpul:
La sfârșitul celei de a patra a doua viteza unghiulară este:
\ [\ Omega \ din stânga (t = 4 \ dreapta) = 10 \ cdot 4 = 40 \ \ stânga (\ frac \ dreapta). \]
Folosind expresia (1.1), vom găsi amploarea accelerației centripete:
Sarcină. Miscarea punctului material este dată de ecuația: $ \ overline \ stânga (t \ dreapta) = 0,5 \ (\ overline \>) $, unde $ \ omega = 2 \ \ frac $. Care este magnitudinea punctului de accelerație normală?
Decizie. Ca bază pentru rezolvarea problemei va lua definiția accelerației centripete sub formă de:
Se vede din condițiile problemei, că traiectoria de mișcare a unui punct este un cerc. În ecuația parametrică forma: $ \ overline \ stânga (t \ dreapta) = 0,5 \ (\ overline \>) $, unde $ \ omega = 2 \ \ frac $ poate fi reprezentat ca:
Raza traiectoriei poate fi definită ca:
Componentele vitezei sunt:
Primirea de viteză modul:
Viteza de valoare și substitut raza unui cerc în expresia (2.2), avem: