Prima parte a fost considerată o metodă pentru a găsi matricea inversă prin cofactori. Aici vom descrie o metodă pentru identificarea unei matrici inverse folosind transformările de eliminare Gauss și Gauss-Jordan. Adesea, această metodă de a găsi metoda matricei inverse numite transformări elementare.
Metoda de transformări elementare
Pentru a utiliza această metodă într-o matrice înregistrată matrice predeterminate $ O matrice $ identitate și $ E $, adică constituie matricea de forma $ (A | E) $ (această matrice este, de asemenea, numit extins). După aceea, cu ajutorul unor transformări elementare realizate cu matrice de siruri de caractere augmentată, aceasta se realizează faptul că matricea din partea stângă a caracteristicilor va fi un singur, cu matricea extinsă ia forma $ \ stânga (E | A ^ \ dreapta) $. Prin transformări elementare în această situație includ aceste acțiuni:
- Schimbarea două rânduri de scaune.
- Multiplicarea toate elementele rând într-un număr nu este egal cu zero.
- Adăugarea elementelor elementelor corespunzătoare de un rând de alt rând înmulțit cu orice factor.
Aplicați transformările elementare pot în diferite moduri. De obicei, selectat Gauss sau metoda de eliminare Gauss-Jordan. În general, metodele Gauss si Gauss-Jordan proiectat pentru a rezolva sisteme de ecuatii algebrice liniare, nu pentru a găsi matrici inverse. Expresia „aplicarea eliminării Gaussian pentru a găsi matricea de feedback“ aici trebuie înțeles ca „operațiunile de aplicare inerente metodei Gauss, pentru a găsi matricea inversă.“
exemple de numerotare continua cu prima parte. În exemplele discutate №5 și №6 folosesc eliminarea gaussiană pentru a găsi matricea inversă, ca în exemplele №7 și №8 analizat folosind metoda lui Gauss-Jordan. Rețineți că, dacă în timpul soluțiile toate elementele unui rând sau o coloană a matricii aranjate pentru caracteristici reseta la zero, matricea inversă nu există.
Găsiți matricea $ A ^ $, în cazul în care $ A = \ la stânga (\ începe 7 4 6 \\ 2 5 -4 \\ 1 -1 3 \ end \ dreapta) $.
Acest exemplu este găsit metoda Gauss inverse. Matricea extinsă având forma generală de $ (A | E) $, în acest exemplu, să ia o formă: $ \ stânga (\ începe 7 4 6 1 0 0 \\ 2 5 -4 0 1 0 \\ 1 -1 3 0 0 1 \ end \ dreapta) $.
Scopul: folosind transformări elementare cauza matrice extinse la forma $ \ left (E | A ^ \ dreapta) $. Vom aplica aceleași etape care sunt utilizate pentru sisteme de ecuații liniare de rezolvare Gauss. Pentru aplicarea metodei Gauss este utilă atunci când primul element al primului rând este extins unitatea de matrice. Pentru a realiza acest lucru, am interchange primul și al treilea rând al matricei augmentată, care va fi aceasta: $ \ stânga (\ începe 1 -1 3 0 0 1 \\ 2 5 -4 0 1 0 \\ 7 4 6 1 0 0 \ end \ dreapta) $.
Vom începe o decizie. Gauss este împărțit în două etape: cursa de avans și o întoarcere (o descriere detaliată a metodei pentru sistemele de ecuații în exemplele filete relevante de rezolvare). Aceste două etape vor fi aplicate în procesul de găsire a matricei inverse.
drept curs
Cu elemente din zero, din primul rând al primei coloane, situată sub prima linie:

În mod similar, acțiunea este realizată și $ III-7 \ cdot I $. Dacă aveți dificultăți cu punerea în aplicare a acestor operațiuni, acestea pot fi efectuate separat (similar cu cel prezentat o acțiune $ II-2 \ cdot I $ de mai sus), iar rezultatul este apoi pentru a face matricea extinsă.
Cu al doilea rând de-al doilea element coloană zeroize dispus sub al doilea rând:
Se împarte linia a treia 5:
Inainte de a rula peste. Toate elementele sub diagonala principală a matricei caracteristicilor, zero.
inversare
Cu elemente din zero al coloanei treilea rând treia situat deasupra a treia linie:
Înainte de a trece la etapa următoare secțiunea a doua linie $ 7 $:
Cu elemente din zero al coloanei a doua linie a doua poziționat deasupra al doilea rând:
Conversia este terminată, matricea inversă a metodei Gauss este găsit: $ A ^ = \ stânga (\ începe -11/5 18/5 46/5 \\ 2 -3 -8 7/5 \\ -11/5 -27/5 \ end \ dreapta) $. Verificați, dacă este necesar, se poate face la fel ca în exemplele precedente. Dacă săriți peste toate explicațiile, soluția ia forma:

Răspuns. $ A ^ = \ left (\ începe -11/5 18/5 46/5 \\ 2 -3 -8 7/5 \\ -11/5 -27/5 \ end \ dreapta) $.
Găsiți matricea $ A ^ $, în cazul în care $ A = \ left (\ începe -5 4 1 0 \\ 2 3 -2 1 \\ 0 7 -4 -3 \\ 1 4 0 6 \ end \ dreapta) $.
drept curs

Conversia cursei înainte finalizată. Toate elementele sub diagonala principală a matricei din partea stângă a caracteristicilor, reset.
inversare

Matricea inversă a metodei Gauss este găsit, $ A ^ = \ stânga (\ începe -13/14 -75/8 31/8 7/2 -19/8 \\ -117/16 49/16 11/4 -23/4 \\ -141/8 57/8 \\ 13/2 17/8 103/6 -43/16 -9/4 \ end \ dreapta) $. Verificați, dacă este necesar, să efectueze în același mod ca și în exemplele №2 și №3.
Răspuns. $ A ^ = \ left (\ începe -13/14 -75/8 31/8 7/2 -19/8 \\ -117/16 49/16 11/4 -23/4 \\ -141/8 57/8 \\ 13/2 17/8 103/6 -43/16 -9/4 \ end \ dreapta) $.
Găsiți matricea $ A ^ $, în cazul în care $ A = \ stânga (\ începe 2 3 4 \\ 7 1 9 \\ -4 5 -2 \ end \ dreapta) $.
Pentru a găsi operația de matrice inversă este metoda tipică aplicabilă de eliminare Gauss-Jordan. Spre deosebire de metoda Gauss, discutate în exemplele precedente №5 și №6. Este că decizia este efectuată într-o singură etapă. Permiteți-mi să vă reamintesc că metoda Gauss este împărțit în două etape: cursa de avans ( „a face“ zerouri sub diagonala principală a matricei la linia) și invers (zero în elementele de pe diagonala principală a matricei la linia). Pentru a calcula matricea inversă a metodei Gauss-Jordan a două soluții nu este necesară pași. Pentru a începe cu o serie extinsă: $ (A | E) $:
$$ (A | E) = \ left (\ 2 începe 3 4 1 0 0 \\ 7 1 9 0 1 \\ 0 -4 5 -2 0 0 1 \ end \ dreapta) $$
Resetați toate intrările din prima coloană, dar una. În prima coloană, toate elementele sunt nenul, prin urmare, pot alege orice element. Să luăm, de exemplu, $ (- 4) $:
Selectată elementul $ (- 4) $ este pe a treia linie, prin urmare, este a treia linie folosim pentru a reseta elementele selectate din prima coloană:
Să facem primul element al treilea rând a devenit egal cu unu. Pentru a face acest lucru, împărțiți al treilea rând al elementelor matricei augmentate de $ (- 4) $:
Vom începe resetarea elementelor corespunzătoare ale primei coloane:
În măsuri suplimentare pentru a utiliza al treilea rând va fi deja imposibil, pentru că suntem deja utilizate în prima etapă.
Am ales un element non-zero, a doua coloană și zero, toate celelalte elemente ale a doua coloană. Putem alege oricare dintre cele două elemente: $ \ frac $ sau $ \ frac $. Elementul de $ \ stânga (- \ frac \ dreapta) $ nu poate fi selectat, deoarece este situat pe a treia linie, pe care am folosit în etapa anterioară. Alege un $ \ $ Frac elementul, care este situat în primul rând. Fă-o, astfel că, în loc de $ \ $ Frac în prima linie a fost unitatea:
Acum, zero afară elementele respective ale a doua coloană:
În discuția ulterioară nu poate fi utilizată prima linie.
Ai nevoie pentru a reseta toate elementele din a treia coloană cu excepția unuia. Avem nevoie de a alege un element de bază non-zero, a treia coloană. Cu toate acestea, nu putem lua $ \ frac $ sau $ \ $ Frac, deoarece aceste elemente sunt aranjate în prima și a treia linii, care ne-am obișnuit. Alegerea este limitată: ea rămâne doar un element de $ \ $ Frac, care este situat pe a doua linie. Împărțim toate elementele din al doilea rând, în $ \ frac $:
Acum, zero afară de elementele relevante din coloana a treia:
Transformarea prin metoda lui Gauss-Jordan este terminat. Rămâne doar pentru a face matricea de trăsături pentru a deveni o unitate. Acest lucru va trebui să schimbe ordinea rândurilor. Pentru a începe, am interbancare prima și a treia linii:
$$ \ stânga (\ începe 1 0 0 47/4 -13/2 -23/4 \\ 0 0 1 -39/4 11/2 19/4 \\ 0 1 0 11/2 -3 -5/2 \ end \ dreapta) $$
Acum, schimb doua și a treia linii:
$$ \ stânga (\ începe 1 0 0 47/4 -13/2 -23/4 \\ 0 1 0 11/2 -3 -5/2 \\ 0 0 1 -39/4 11/2 19/4 \ end \ dreapta) $$
Deci, $ A ^ = \ left (\ începe 47/4 -13/2 11/2 -23/4 \\ -3 -5/2 \\ -39/4 11/2 19/4 \ end \ dreapta) $. Desigur, soluția poate fi realizată într-un mod diferit, alegând elemente de pe diagonala principală. De obicei, o face doar asta, pentru că, în acest caz, la sfârșitul deciziei de a nu trebuie să se schimbe o linie în unele locuri. Am dat decizia anterioară cu un singur scop: pentru a arăta că alegerea liniei la fiecare pas nu este critică. Dacă alegeți elementele diagonale, această decizie ar fi astfel la fiecare pas:
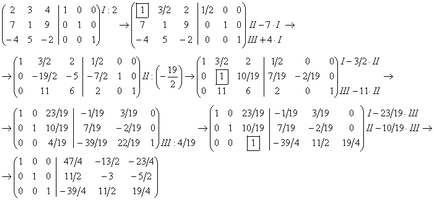
Dintre aceștia din urmă, avem o matrice: $ A ^ = \ left (\ începe 47/4 -13/2 11/2 -23/4 \\ -3 -5/2 \\ -39/4 11/2 19/4 \ end \ dreapta) $
Metoda de Inverse Gauss-Jordan a primit doar scrie răspunsul rămâne.
Răspuns. $ A ^ = \ left (\ începe 47/4 -13/2 11/2 -23/4 \\ -3 -5/2 \\ -39/4 11/2 19/4 \ end \ dreapta) $.
Găsiți matricea $ A ^ $, în cazul în care $ A = \ left (\ începe 1 1 1 0 \\ 2 4 0 1 \\ 0 17 2 \\ -3 -1 4 0 -1 \ end \ dreapta) $.
Cu prima linie care corespunde la zero din elemente în prima coloană:
Folosind rândul al doilea corespunzând la zero din elementele a doua coloană:
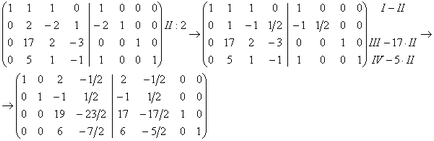
Folosind linia a treia care corespunde zero afară elementelor din coloana a treia:

Folosind al patrulea rând la zero din elementele respective ale patra coloană:

Deci, $ A ^ = \ left (\ începe -16/5 -3/5 8/5 2/5 -27/5 \\ 1/5 -1/5 4/5 \\ 19/5 2/5 -7/5 \\ 23/5 24/5 7/5 -12/5 38/5 \ end \ dreapta) $. Dacă săriți peste toate explicațiile, soluția ia forma:

Răspuns. $ A ^ = \ left (\ începe -16/5 -3/5 8/5 2/5 -27/5 \\ 1/5 -1/5 4/5 \\ 19/5 2/5 -7/5 \\ 23/5 24/5 7/5 -12/5 38/5 \ end \ dreapta) $.
Dacă în cursul soluționării elementului diagonală adus la zero, puteți schimba linia, uneori. De exemplu, într-o matrice $ B = \ stânga (\ începe 1 5 11 10 0 \\ 0 0 9 5 -6 \\ 0 7 1 -1 -3 \\ 0 -11 8 -9 12 \\ 0 0 6 -3 25 \ end \ dreapta) $ elementele corespunzătoare din prima resetare coloană. Este necesar să se procedeze la anularea elementelor din coloana a doua, dar $ B_ = 0 $. Interschimba al doilea și al treilea rând al matricei $ B $: $ \ left (\ 1 începe 5 11 10 0 \\ 0 7 1 -1 -3 \\ 0 0 9 5 -6 \\ 0 -11 8 -9 12 \\ 0 0 6 -3 25 \ end \ dreapta) $. Acum, în loc de zero, avem numărul 7 și continuând în continuare metoda de transformare standard, Gauss-Jordan eliminare.
Dacă sunteți interesat în metoda de calcul matricei inverse folosind cofactori, descrierea acestei metode este în prima parte.