Text Lecții de decodare:
În planimetrie unul dintre obiectele de studiu este unghiul.
Unghi - o figură geometrică compusă din puncte - vârful și două raze care provin din acest punct.
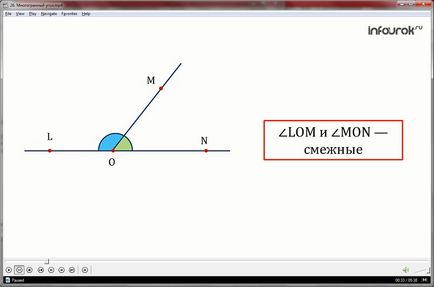
Două unghiuri, una dintre părți care este generală, iar celelalte două sunt o continuare unul de celălalt, în geometria plan numit adiacente.
Busola poate fi privit ca un model de unghi plan.
Să ne amintim conceptul de unghi diedru.
Această cifră formată de linia A, și două jumătăți de avioane din comună limita și care nu fac parte din aceeași geometrie plan numit unghiul diedru. Semiplan - este marginea unghiului diedru. Linia a - o nervură de un unghi diedru.
Acoperișul casei demonstrează unghiul diedru.
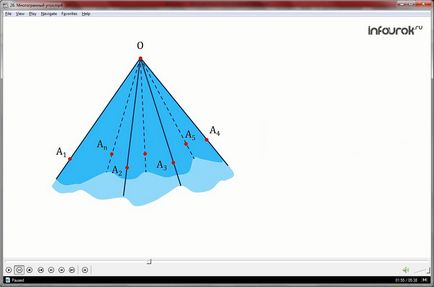
Dar acoperișul casei în figura doi este sub forma unei figuri format de șase avion cu un vârf comun unghiuri, astfel încât unghiurile sunt luate într-o anumită ordine, iar fiecare pereche de colțuri adiacente, inclusiv primul și ultimul, are o latură comună. Cum se numește această formă de acoperiș?
Cifra geometrie, compusă din unghiurile
A1OA2, și așa mai departe A2OA3 AnOA1 și regiunile interne, astfel încât cele adiacente nu sunt coplanare, mai degrabă decât unghiuri adiacente (cu zonele lor interne) nu au puncte comune numit unghi poliedrică OA1A2 A3 ... A n.
A colțuri din care acest unghi este numit colțuri plate. Partea de unghiurile plane se numesc muchii ale unghiului poliedrică. Punctul O se numește vârful unghiului.
Exemple de unghiuri poliedrice pot fi găsite în tetraedru și paralelipipedice.
Fațetele tetraedru DBA, forma ABC, DBC unghi poliedrică VADC. Cel mai adesea este numit unghi triedru.
În AA1D1D paralelipipedic chipuri, ABCD, generatoare AA1B1B unghi triedru AA1DB.
Ei bine, acoperișul casei este realizat sub forma unui unghi hexagonal. Se compune din șase unghiuri plane.
Pentru unghiul poliedrică deține un număr de proprietăți. Noi formuleze și să le dovedească. Se spune aici că declarația

În primul rând, pentru orice unghi poliedrică convexă există un plan care intersectează toate coastele lui.
Luați în considerare dovezile pentru unghiul poliedrică OA1A2 A3 ... A n.
Prin ipoteză, este convexă. Unghiul se numește convexă dacă se află pe o parte a planului de fiecare dintre unghiurile sale plane.
Deoarece prin ipoteza de colț convex, punctele O, A1, A2, A3 până la An sunt pe de o parte a OA1A2 avionul
Desenați linia mediană OA1A2 KM triunghi și de a alege de la marginile OA3 OA4, Oan nervura care formează cu planul RCM, cel mai mic unghi diedru. Să fie o muchie OAI. (Oa itoe)
Să considerăm o jumătate APPa cu delimitare CM împărțind unghiul diedru OKMAi două unghi diedru. Toate nodurile A la A n minciună pe de o parte a plane α, iar punctul D pe cealaltă parte. Prin urmare, planul α intersectează toate muchiile unghiului poliedrică. Afirmația este dovedită.
Unghiurile poliedrice Convex au o altă proprietate importantă.
unghiuri cantitate plane dintr-un unghi de poliedrică convex mai mic decât 360 °.

Luați în considerare un unghi de poliedric convex cu vârful în punctul O. Prin declarațiile de mai sus există un plan care intersectează toate marginile sale.
Desenează un plan α, lăsați-l intersectează marginile punctelor de unghi A1, A2, A3 la An, și așa mai departe.
Plane α din zona exterioară să fie tăiat unghi plan triunghi. Suma unghiurilor este de 180 °. Considerăm că suma unghiurilor plane de A1OA2 la exprimare AnOA1 este transformat de această expresie a rearanja termeni, obținem
În această expresie sume în paranteze sunt cantități unghiuri plane triunghiulare de colț, și după cum știți acestea sunt mai mari decât unghiul de-al treilea plan.
Această inegalitate poate fi scrisă pentru toate colțurile triedru care formează unghiul poliedrică.
În consecință, obținem continuarea egalității
Răspunsul primit arată că suma unghiurilor plane ale unui unghi de poliedrică convexă mai mică de 360 de grade.