Formula la = k / x. Programul este o hiperbolă. În partea 1 a DPA, această funcție este oferită fără deplasare de-a lungul axelor. Prin urmare, acesta are un singur parametru k. Cea mai mare diferență în aspectul graficului depinde de semnul k.
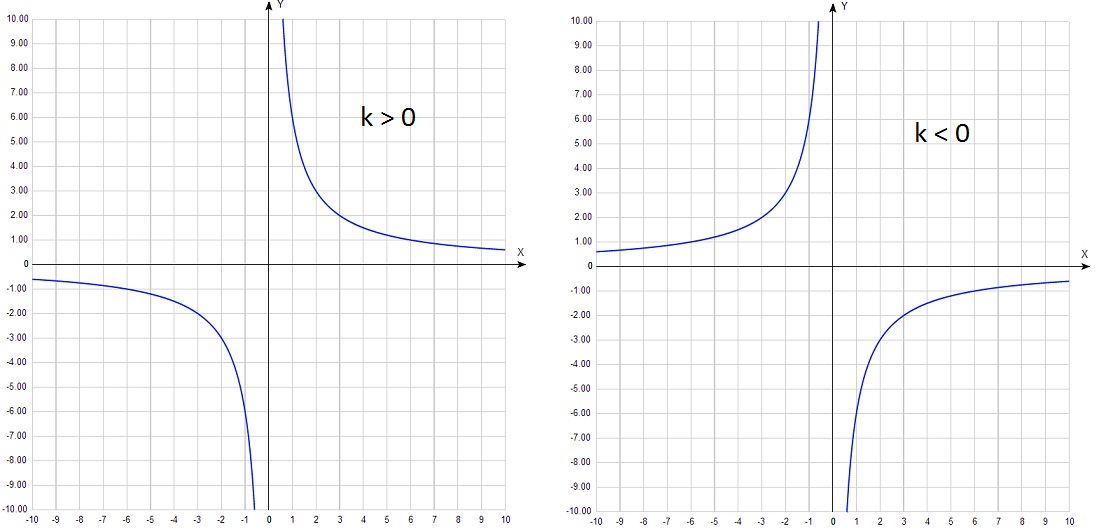
Este mult mai dificil de a vedea diferențele din grafice, în cazul în care k este un semn:
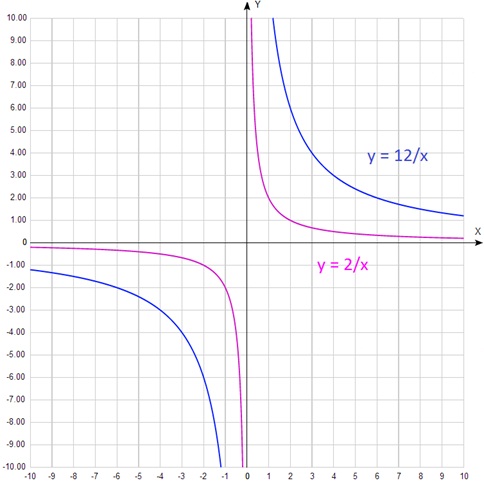
După cum putem vedea, decât mare k. Ea se extinde deasupra hiperbola.
Figura prezintă funcțiile pentru care parametrul k diferă în mod semnificativ. În cazul în care diferența nu este atât de mare, încât este destul de dificil să se determine cu ochiul liber.
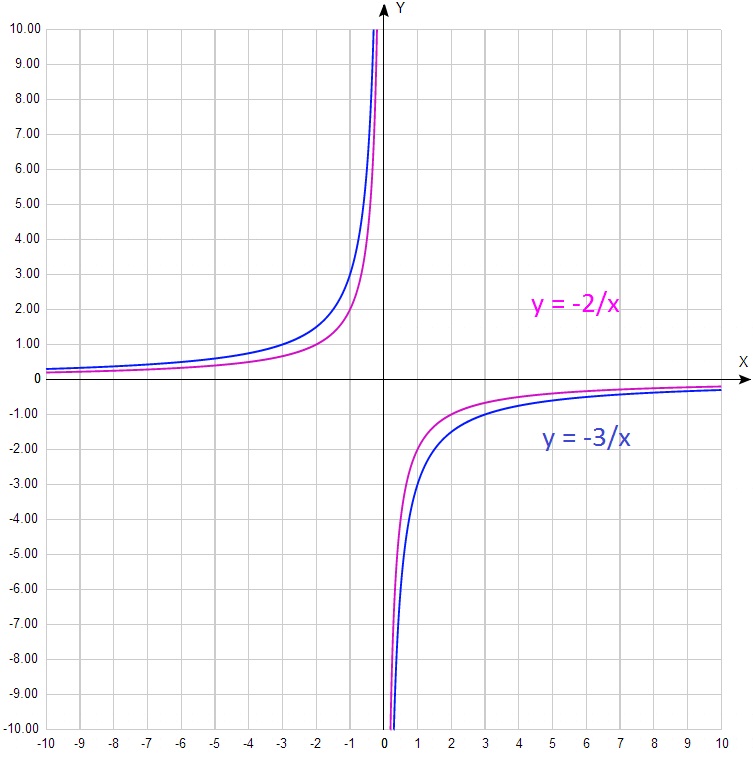
În acest sens, o „capodopera“ este următoarea lucrare, mi-a găsit într-un tutorial în general bun pe pregătirea pentru DPA:

Nu numai că, imaginea destul de bine grafica spațiate strâns îmbinare pur și simplu. Deci, chiar hiperbola cu kizobrazheny pozitive și negative într-un plan de coordonate. Care confundă complet oricine care ia o privire la această imagine. doar „stea rece“ este izbitoare.
Slavă Domnului, este doar o activitate de formare. În exemplele de realizare actuale, a oferit formulare mai corectă și desene evidente.
Vom înțelege modul de a determina coeficientul k sub funcția de program.
Din formula: y = k / x, rezultă că k = y · x. Adică, putem lua orice punct de coordonate întregi cu confortabil și să le multiplice - se obține k.
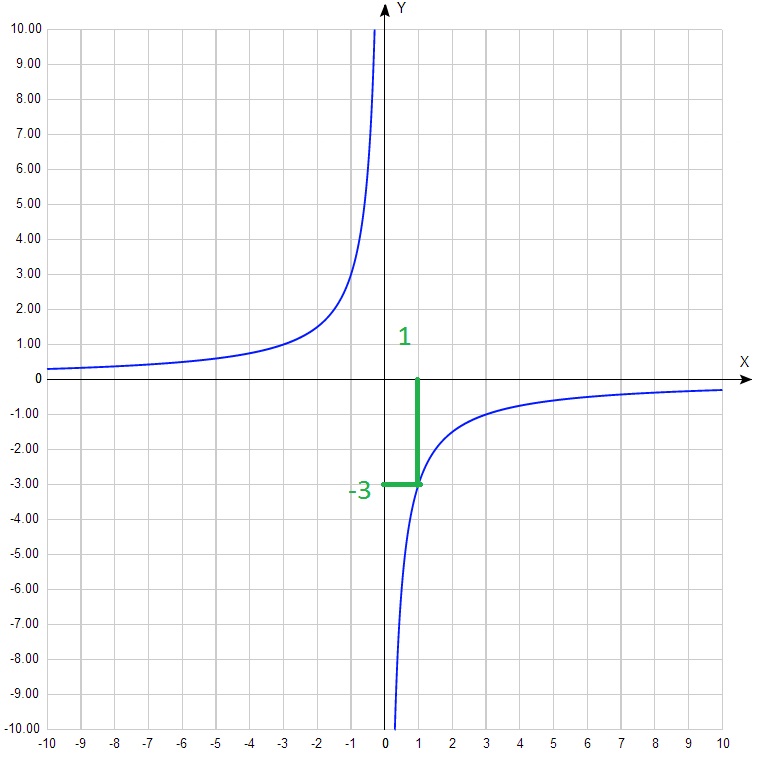
k = 1 + (- 3) = - 3.
Formula deci această funcție: y = - 3 / x.
Este interesant să ia în considerare situația cu k fracționată. În acest caz, formula poate fi exprimată în mai multe moduri. Nu ar trebui să inducă în eroare.
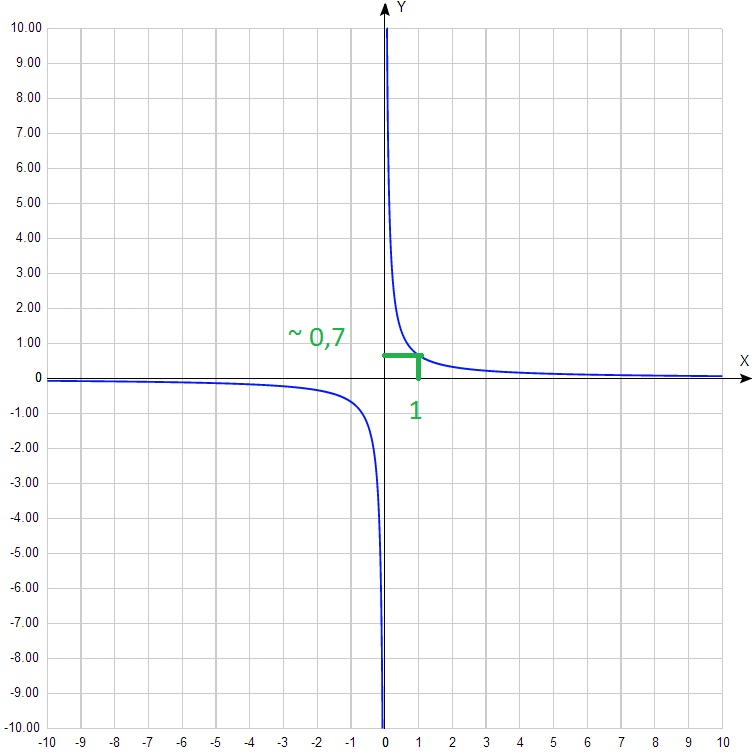
Această diagramă este imposibil de a găsi un singur punct întreg. Prin urmare, valoarea k poate fi determinată foarte aproximativ.
k = 1 · 0,7≈0,7. Cu toate acestea, putem vedea că 0
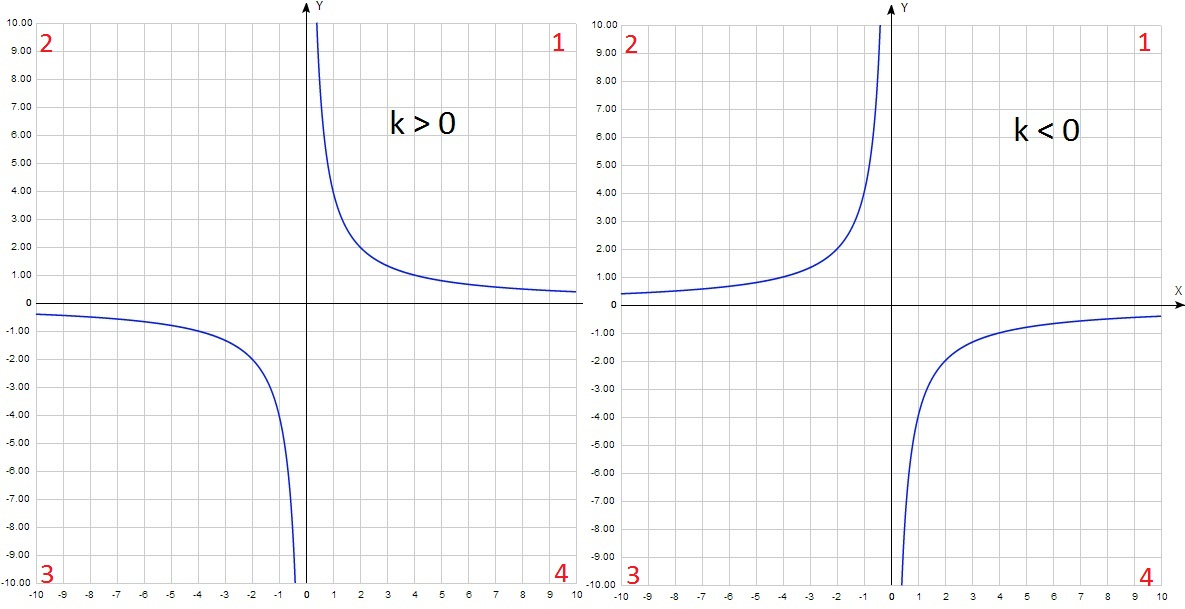
k> 0 este o hiperbolă în 1 și 3 coordonate unghiurile (cadrane)
k <0 – во 2-м и 4-ом.
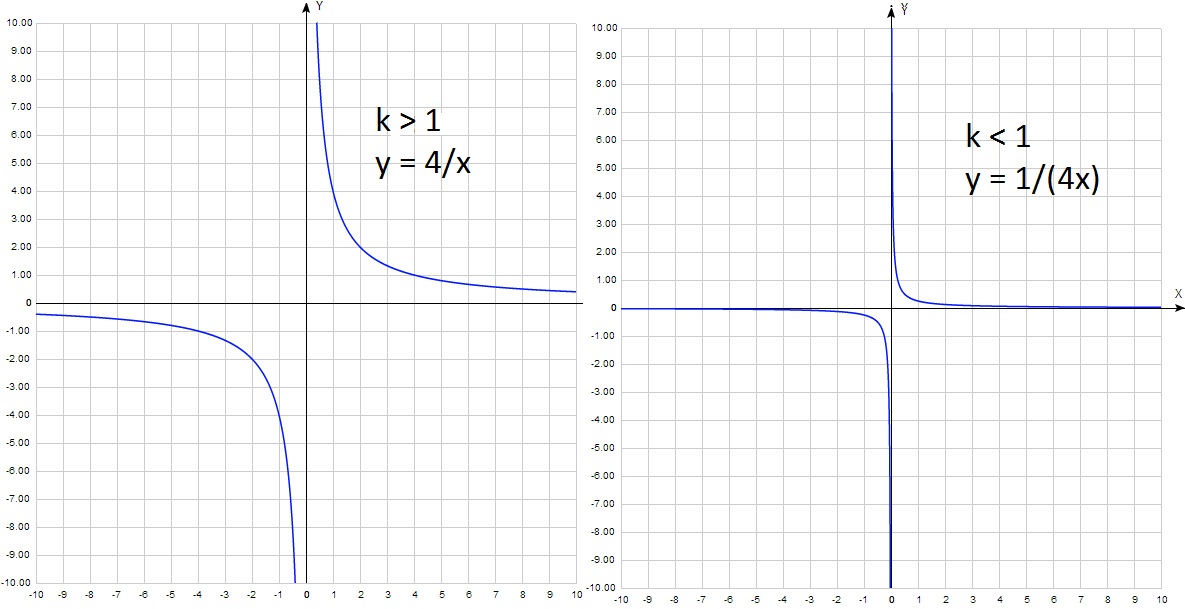
Dacă k este mai mare de 1 modulo (k = 2 sau k = - 2), graficul este mai mare de 1 (de mai jos - 1) pe axa y, este mai larg.
Dacă k este mai mică de 1 modulo (k = 1/2 sau k = - 1/2), atunci graficul este mai mic de 1 (de mai sus - 1) pe axa Y și este mai îngust, "presat" la zero:
Luați în considerare problema, propusă într-un exemplu de realizare a APD:
Potriviți graficele funcțiilor și formulele care le definesc.
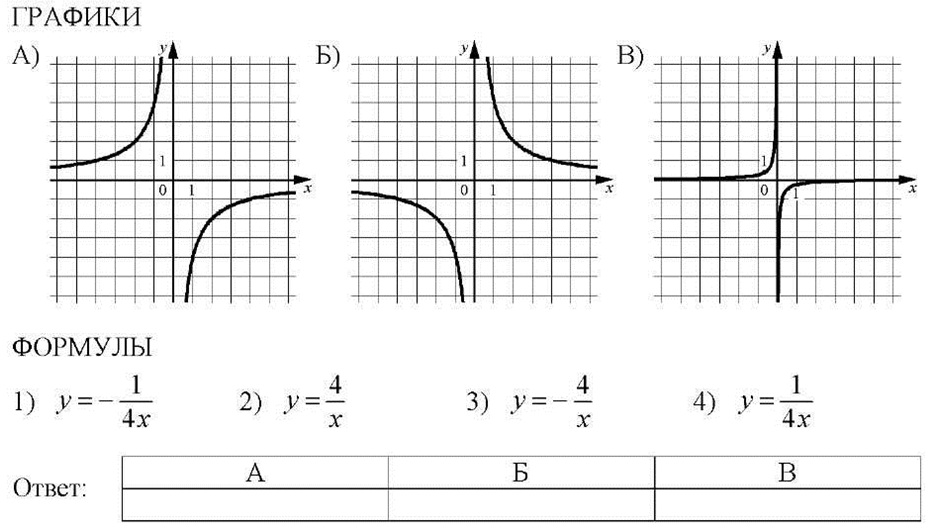
A) În conformitate cu localizarea hiperbole în a doua și a patra colțurile coordonate, putem concluziona că k <0. Этому условию отвечают формулы 1) и 3). График располагается выше у = 1, поэтому k>1 al modulului, adică 3)
B) Conform poziției hiperbola în prima și a treia coordonate unghiurile putem concluziona că k> 0. Această condiție corespunde formulei 2) și 4). Program este deasupra y = 1, deci k> 1 modulo, adică 2)
B) în funcție de locația hiperbole în a doua și a patra colțurile coordonate, putem concluziona că k <0. Этому условию отвечают формулы 1) и 3). График располагается ниже у = 1, поэтому k <1 по модулю, то есть 1)