Exemple de rezolvare a problemelor
142. Găsiți lungimea cercului circumscris despre partea trapezoidală care este, o, a și 2a (Fig. 200). (1)
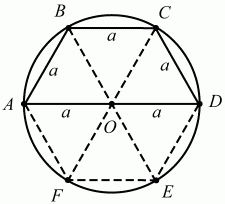
Decizie. Este ușor de observat că ABCD trapez poate fi extinsă la un hexagon regulat (vezi fig ..) Dar raza hexagon regulat al cercului circumscris este partea hexagonului: Rokr = a. circumferința lungime l = 2? ROKR = 2 a.
143. bază trapez este de 4 cm și 9 cm, iar diagonala sunt de 5 cm și 12 cm. Gasiti zona trapezului, iar unghiul dintre diagonalele sale (fig. 201). (2)
Decizie. Să ABCD - acest trapez, CD = 4 cm, 9 cm = AB, BD = 5 cm și 12 cm AC = elemente cunoscute pentru a fi incluse într-un triunghi, fast forward diagonal BD-vector comutator DC SW „.. Luați în considerare triunghiul ACB“. Deoarece VV'CD - un paralelogram, apoi B'C = 5 cm, AB = AB + BB = AB + CD = 13 cm, este cunoscut acum pentru toate cele trei laturi ale triunghiului AB'C .. Deoarece TT2 + V'S2 = (AB ') 2 = 52+ 122 = 132, triunghiul AB'C - dreptunghiular, iar DIA' = 90 °. Rezultă imediat că unghiul dintre diagonalele trapezului, egal cu unghiul ACB „este de 90 °. Zona trapezului, din nici un patrulater diagonalele egală cu jumătate din produsul din sinusul unghiului dintre ele. Din acest domeniu este egal cu 1 / 2AC. BD. păcat 90 ° = 1/2. 12. 5. 1 = 30 cm2.
A: 30 cm2, 90 °.
144. Ground AB trapez ABCD este de două ori mai lung și de două ori pe CD baze AD din partea laterală mai lungă. Lungimea AU diagonalei egală cu a, iar lungimea BC lateral este egal cu b. Găsiți aria unui trapez (fig. 202). (3)
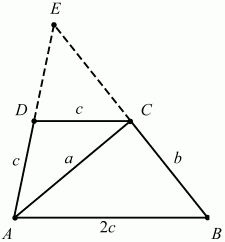
Decizie. Să AB = 2c, atunci CD = AD = a. Extindeți laturile BC AD pentru a le intersectează într-un punct E. obține triunghi BAE. Deoarece CD = 1 / 2AV, CD - linia medie a triunghiului Abe. Rezultă că CE = BC = b, și DE = AD = a. Sa dovedit că AB = AE. Prin urmare, triunghiul este isoscel și BAE AC - media lui. Dar într-un triunghi echilateral, mediana efectuat la sol este mare, astfel încât zona BAE a triunghiului poate fi calculată după cum urmează:
Mai departe, t. Pentru. DCE și triunghiuri cu un coeficient EBA similaritate k = 1/2, atunci suprafața DCE triunghiului este 1/4 aria triunghiului Abe (raportul dintre suprafața de factor triunghiuri similaritate similare egal cu pătrat). Zona de trapez este deci egală cu 3/4 din suprafața triunghiului Abe, care este egal cu 3 / 4ab
145. În cadrul unui triunghi echilateral ABC punct dat M astfel încât AM = 1, BM = a3 și CM = 2. Găsiți lungimea AB (Fig. 203). (3)
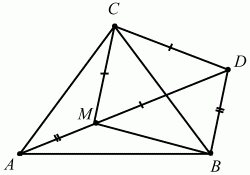
Decizie. Povernom AFM triunghi în jurul punctului C de 60 °. Apoi, punctul A se va deplasa la punctul B, litera M - într-un punct D, AFM triunghi - un triunghi BCD. ? În acest caz, CD-ul și CM = MCD = de 60 °, prin urmare, CDM triunghiul - echilateral, și, prin urmare CDM = DMC = 60 ° ??. Folosind obținut strunjire triunghiul auxiliar BDM. Rețineți că BD = AM = 1 = VM? 3, DM = CM = 2. Prin urmare, în unghi-BDM triunghi (de fapt BM2 + BD2 = (? 3) 2 + 12 = DM2). DBM = 90 ° și? BMD = 30 ° (BD laterale opuse este egală cu jumătate din ipotenuza MD). În continuare vom calcula unghiul DIU. Navy =? BMD +? DMC = 30 ° + 60 ° = 90 °. Aplicând teorema lui Pitagora la BCM triunghi, descoperim că